Recurrent switching linear dynamical systems
Paper and Code
Oct 26, 2016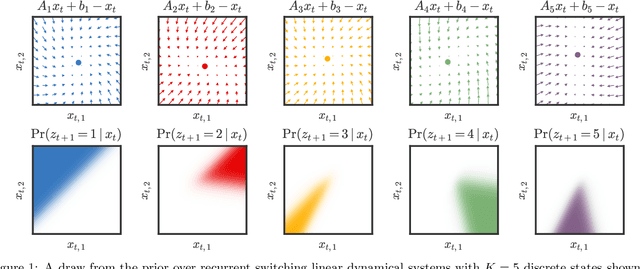
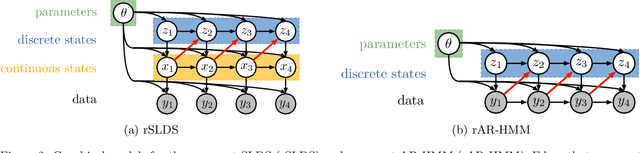
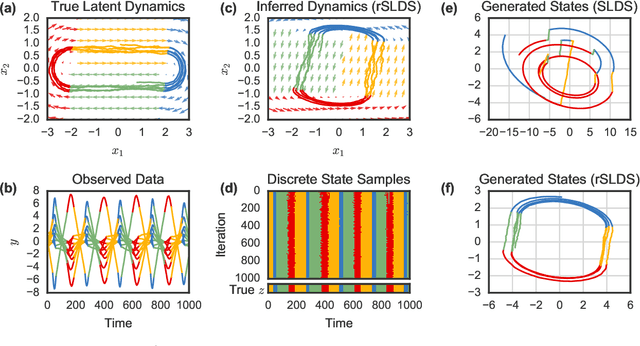

Many natural systems, such as neurons firing in the brain or basketball teams traversing a court, give rise to time series data with complex, nonlinear dynamics. We can gain insight into these systems by decomposing the data into segments that are each explained by simpler dynamic units. Building on switching linear dynamical systems (SLDS), we present a new model class that not only discovers these dynamical units, but also explains how their switching behavior depends on observations or continuous latent states. These "recurrent" switching linear dynamical systems provide further insight by discovering the conditions under which each unit is deployed, something that traditional SLDS models fail to do. We leverage recent algorithmic advances in approximate inference to make Bayesian inference in these models easy, fast, and scalable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge