Fast Debiasing of the LASSO Estimator

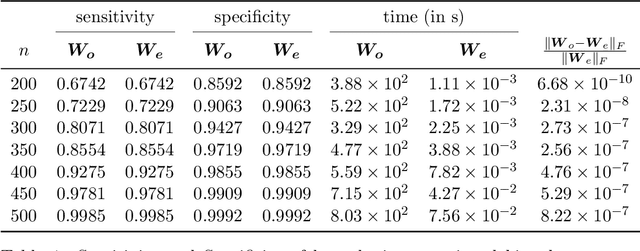
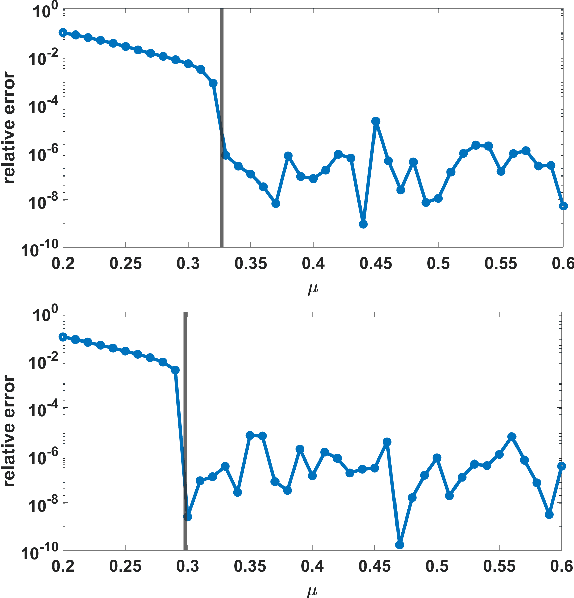
In high-dimensional sparse regression, the \textsc{Lasso} estimator offers excellent theoretical guarantees but is well-known to produce biased estimates. To address this, \cite{Javanmard2014} introduced a method to ``debias" the \textsc{Lasso} estimates for a random sub-Gaussian sensing matrix $\boldsymbol{A}$. Their approach relies on computing an ``approximate inverse" $\boldsymbol{M}$ of the matrix $\boldsymbol{A}^\top \boldsymbol{A}/n$ by solving a convex optimization problem. This matrix $\boldsymbol{M}$ plays a critical role in mitigating bias and allowing for construction of confidence intervals using the debiased \textsc{Lasso} estimates. However the computation of $\boldsymbol{M}$ is expensive in practice as it requires iterative optimization. In the presented work, we re-parameterize the optimization problem to compute a ``debiasing matrix" $\boldsymbol{W} := \boldsymbol{AM}^{\top}$ directly, rather than the approximate inverse $\boldsymbol{M}$. This reformulation retains the theoretical guarantees of the debiased \textsc{Lasso} estimates, as they depend on the \emph{product} $\boldsymbol{AM}^{\top}$ rather than on $\boldsymbol{M}$ alone. Notably, we provide a simple, computationally efficient, closed-form solution for $\boldsymbol{W}$ under similar conditions for the sensing matrix $\boldsymbol{A}$ used in the original debiasing formulation, with an additional condition that the elements of every row of $\boldsymbol{A}$ have uncorrelated entries. Also, the optimization problem based on $\boldsymbol{W}$ guarantees a unique optimal solution, unlike the original formulation based on $\boldsymbol{M}$. We verify our main result with numerical simulations.

Robust Non-adaptive Group Testing under Errors in Group Membership Specifications

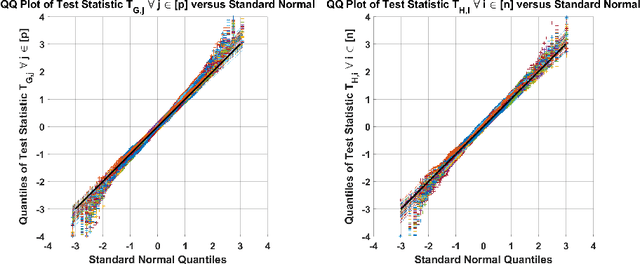
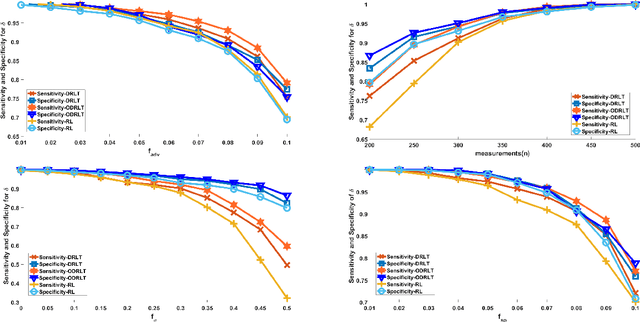
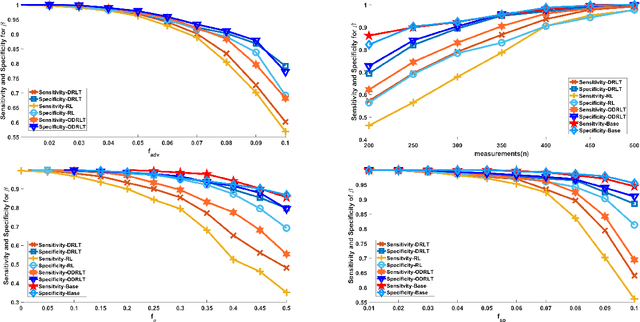
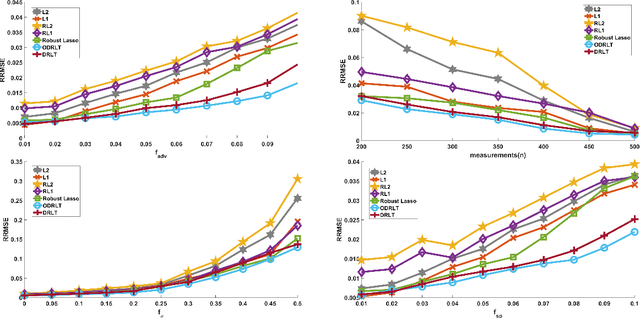
Given $p$ samples, each of which may or may not be defective, group testing (GT) aims to determine their defect status by performing tests on $n < p$ `groups', where a group is formed by mixing a subset of the $p$ samples. Assuming that the number of defective samples is very small compared to $p$, GT algorithms have provided excellent recovery of the status of all $p$ samples with even a small number of groups. Most existing methods, however, assume that the group memberships are accurately specified. This assumption may not always be true in all applications, due to various resource constraints. Such errors could occur, eg, when a technician, preparing the groups in a laboratory, unknowingly mixes together an incorrect subset of samples as compared to what was specified. We develop a new GT method, the Debiased Robust Lasso Test Method (DRLT), that handles such group membership specification errors. The proposed DRLT method is based on an approach to debias, or reduce the inherent bias in, estimates produced by Lasso, a popular and effective sparse regression technique. We also provide theoretical upper bounds on the reconstruction error produced by our estimator. Our approach is then combined with two carefully designed hypothesis tests respectively for (i) the identification of defective samples in the presence of errors in group membership specifications, and (ii) the identification of groups with erroneous membership specifications. The DRLT approach extends the literature on bias mitigation of statistical estimators such as the LASSO, to handle the important case when some of the measurements contain outliers, due to factors such as group membership specification errors. We present numerical results which show that our approach outperforms several baselines and robust regression techniques for identification of defective samples as well as erroneously specified groups.

A Projection Method for Metric-Constrained Optimization

We outline a new approach for solving optimization problems which enforce triangle inequalities on output variables. We refer to this as metric-constrained optimization, and give several examples where problems of this form arise in machine learning applications and theoretical approximation algorithms for graph clustering. Although these problem are interesting from a theoretical perspective, they are challenging to solve in practice due to the high memory requirement of black-box solvers. In order to address this challenge we first prove that the metric-constrained linear program relaxation of correlation clustering is equivalent to a special case of the metric nearness problem. We then developed a general solver for metric-constrained linear and quadratic programs by generalizing and improving a simple projection algorithm originally developed for metric nearness. We give several novel approximation guarantees for using our framework to find lower bounds for optimal solutions to several challenging graph clustering problems. We also demonstrate the power of our framework by solving optimizing problems involving up to 10^{8} variables and 10^{11} constraints.

Estimating the Spectral Density of Large Implicit Matrices

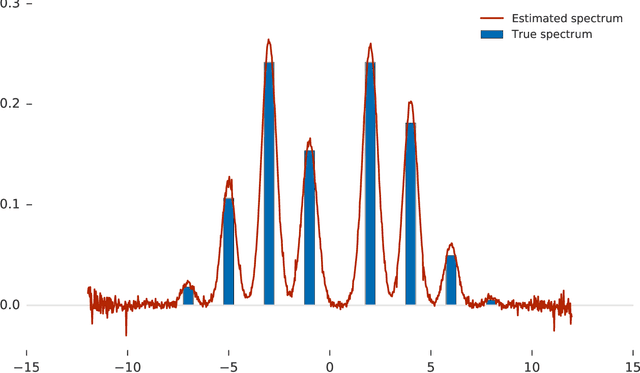
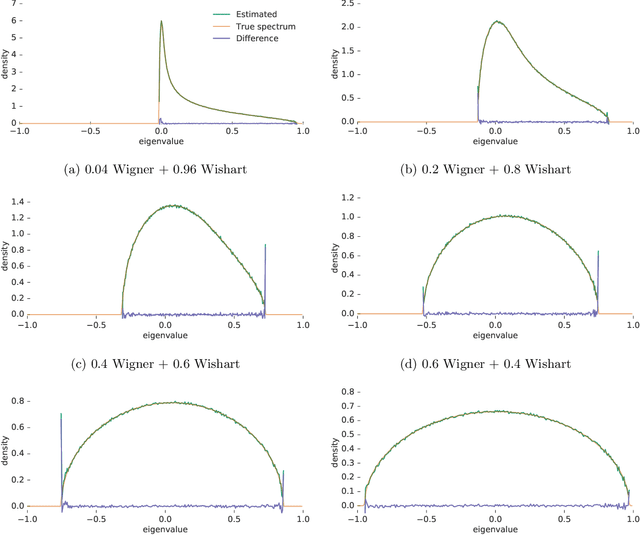
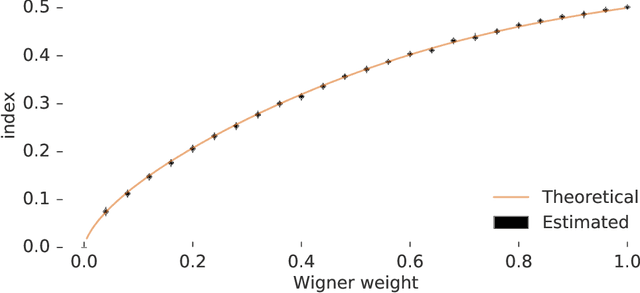
Many important problems are characterized by the eigenvalues of a large matrix. For example, the difficulty of many optimization problems, such as those arising from the fitting of large models in statistics and machine learning, can be investigated via the spectrum of the Hessian of the empirical loss function. Network data can be understood via the eigenstructure of a graph Laplacian matrix using spectral graph theory. Quantum simulations and other many-body problems are often characterized via the eigenvalues of the solution space, as are various dynamic systems. However, naive eigenvalue estimation is computationally expensive even when the matrix can be represented; in many of these situations the matrix is so large as to only be available implicitly via products with vectors. Even worse, one may only have noisy estimates of such matrix vector products. In this work, we combine several different techniques for randomized estimation and show that it is possible to construct unbiased estimators to answer a broad class of questions about the spectra of such implicit matrices, even in the presence of noise. We validate these methods on large-scale problems in which graph theory and random matrix theory provide ground truth.