Parameterized Objectives and Algorithms for Clustering Bipartite Graphs and Hypergraphs

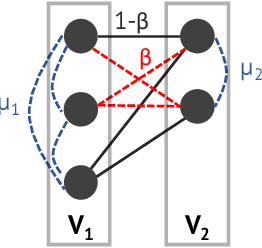
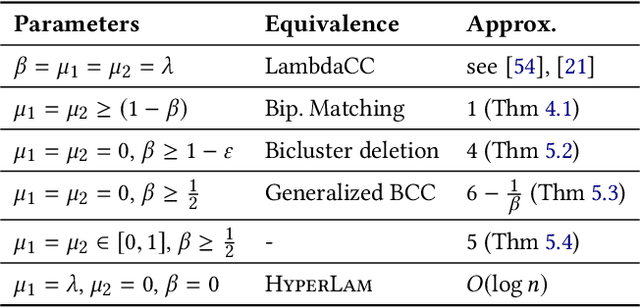
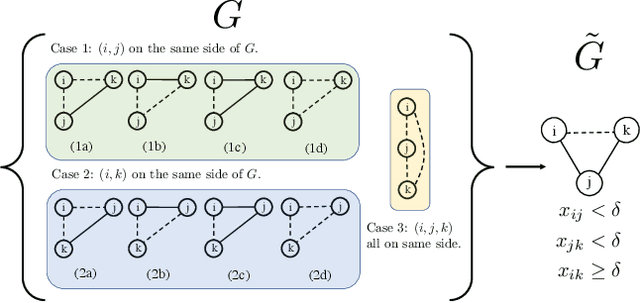
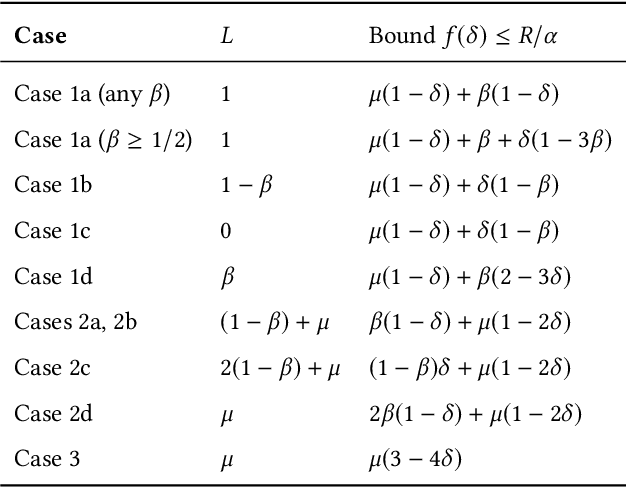
Graph clustering objective functions with tunable resolution parameters make it possible to detect different types of clustering structure in the same graph. These objectives also provide a unifying view of other non-parametric objectives, which often can be captured as special cases. Previous research has largely focused on parametric objectives for standard graphs, in which all nodes are of the same type, and edges model pairwise relationships. In our work, we introduced parameterized objective functions and approximation algorithms specifically for clustering bipartite graphs and hypergraphs, based on correlation clustering. This enables us to develop principled approaches for clustering datasets with different node types (bipartite graphs) or multiway relationships (hypergraphs). Our hypergraph objective is related to higher-order notions of modularity and normalized cut, and is amenable to approximation algorithms via hypergraph expansion techniques. Our bipartite objective generalizes standard bipartite correlation clustering, and in a certain parameter regime is equivalent to bicluster deletion, i.e., removing a minimum number of edges to separate a bipartite graph into disjoint bicliques. The problem in general is NP-hard, but we show that in a certain parameter regime it is equivalent to a bipartite matching problem, meaning that it is polynomial time solvable in this regime. For other regimes, we provide approximation guarantees based on LP-rounding. Our results include the first constant factor approximation algorithm for bicluster deletion. We illustrate the flexibility of our framework in several experiments. This includes clustering a food web and an email network based on higher-order motif structure, detecting clusters of retail products in product review hypergraph, and evaluating our algorithms across a range of parameter settings on several real world bipartite graphs.

Learning Resolution Parameters for Graph Clustering

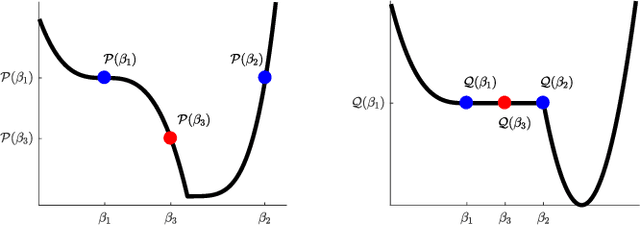
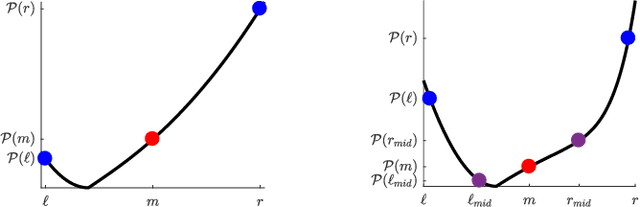
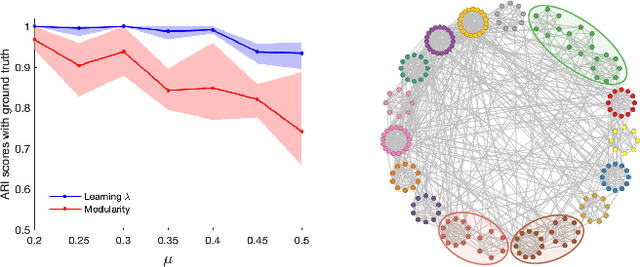
Finding clusters of well-connected nodes in a graph is an extensively studied problem in graph-based data analysis. Because of its many applications, a large number of distinct graph clustering objective functions and algorithms have already been proposed and analyzed. To aid practitioners in determining the best clustering approach to use in different applications, we present new techniques for automatically learning how to set clustering resolution parameters. These parameters control the size and structure of communities that are formed by optimizing a generalized objective function. We begin by formalizing the notion of a parameter fitness function, which measures how well a fixed input clustering approximately solves a generalized clustering objective for a specific resolution parameter value. Under reasonable assumptions, which suit two key graph clustering applications, such a parameter fitness function can be efficiently minimized using a bisection-like method, yielding a resolution parameter that fits well with the example clustering. We view our framework as a type of single-shot hyperparameter tuning, as we are able to learn a good resolution parameter with just a single example. Our general approach can be applied to learn resolution parameters for both local and global graph clustering objectives. We demonstrate its utility in several experiments on real-world data where it is helpful to learn resolution parameters from a given example clustering.

A Projection Method for Metric-Constrained Optimization

We outline a new approach for solving optimization problems which enforce triangle inequalities on output variables. We refer to this as metric-constrained optimization, and give several examples where problems of this form arise in machine learning applications and theoretical approximation algorithms for graph clustering. Although these problem are interesting from a theoretical perspective, they are challenging to solve in practice due to the high memory requirement of black-box solvers. In order to address this challenge we first prove that the metric-constrained linear program relaxation of correlation clustering is equivalent to a special case of the metric nearness problem. We then developed a general solver for metric-constrained linear and quadratic programs by generalizing and improving a simple projection algorithm originally developed for metric nearness. We give several novel approximation guarantees for using our framework to find lower bounds for optimal solutions to several challenging graph clustering problems. We also demonstrate the power of our framework by solving optimizing problems involving up to 10^{8} variables and 10^{11} constraints.

Correlation Clustering with Low-Rank Matrices

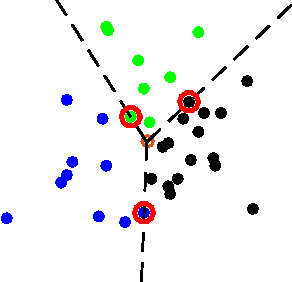
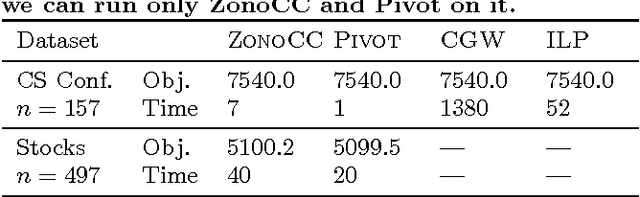
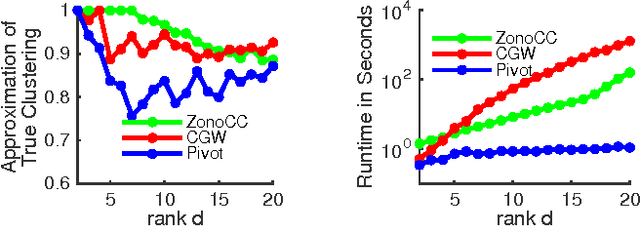
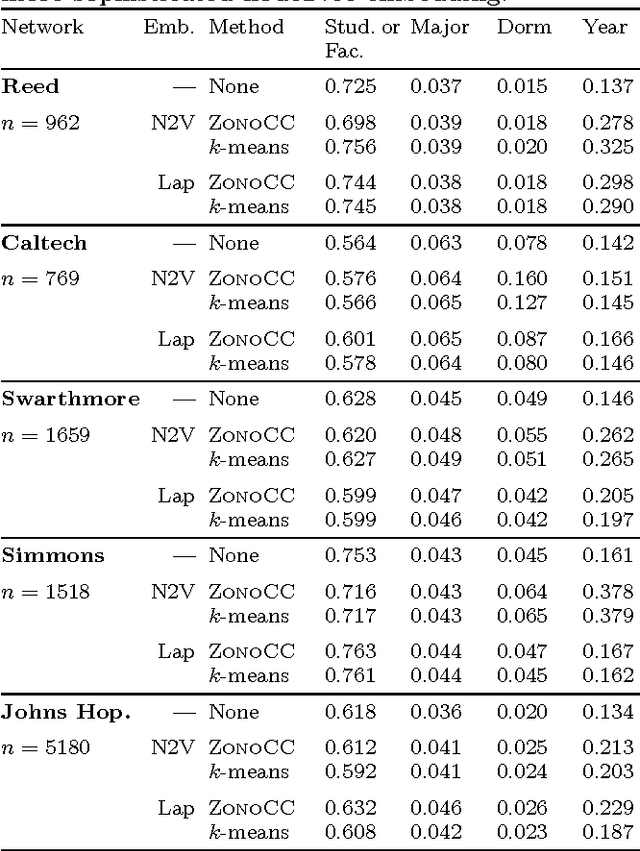
Correlation clustering is a technique for aggregating data based on qualitative information about which pairs of objects are labeled 'similar' or 'dissimilar.' Because the optimization problem is NP-hard, much of the previous literature focuses on finding approximation algorithms. In this paper we explore how to solve the correlation clustering objective exactly when the data to be clustered can be represented by a low-rank matrix. We prove in particular that correlation clustering can be solved in polynomial time when the underlying matrix is positive semidefinite with small constant rank, but that the task remains NP-hard in the presence of even one negative eigenvalue. Based on our theoretical results, we develop an algorithm for efficiently "solving" low-rank positive semidefinite correlation clustering by employing a procedure for zonotope vertex enumeration. We demonstrate the effectiveness and speed of our algorithm by using it to solve several clustering problems on both synthetic and real-world data.