Correlation Clustering with Low-Rank Matrices
Paper and Code
Mar 17, 2017
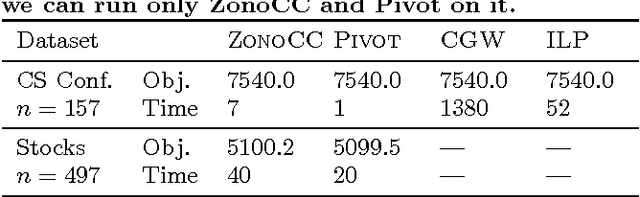
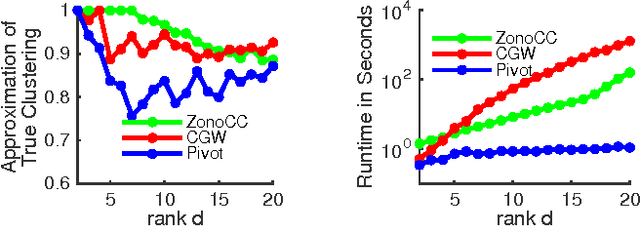
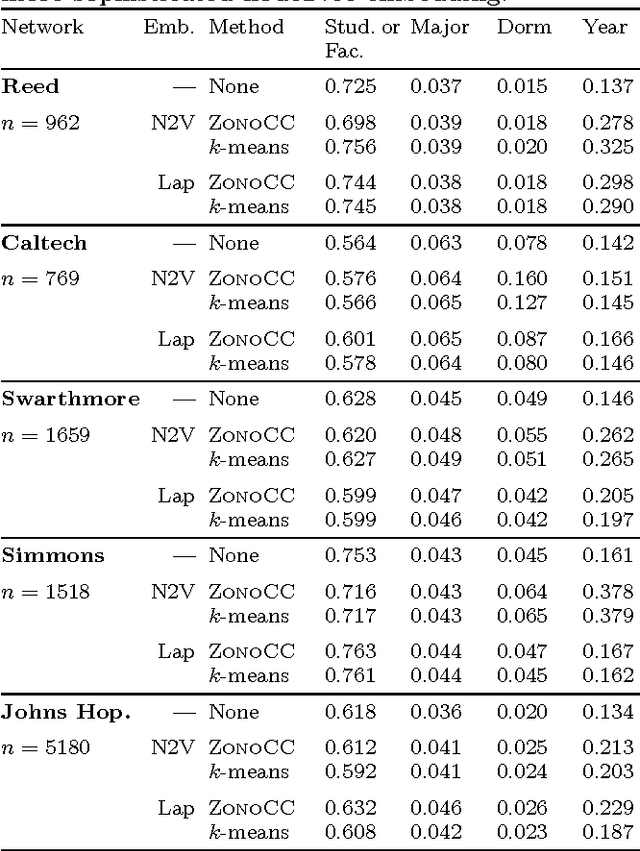
Correlation clustering is a technique for aggregating data based on qualitative information about which pairs of objects are labeled 'similar' or 'dissimilar.' Because the optimization problem is NP-hard, much of the previous literature focuses on finding approximation algorithms. In this paper we explore how to solve the correlation clustering objective exactly when the data to be clustered can be represented by a low-rank matrix. We prove in particular that correlation clustering can be solved in polynomial time when the underlying matrix is positive semidefinite with small constant rank, but that the task remains NP-hard in the presence of even one negative eigenvalue. Based on our theoretical results, we develop an algorithm for efficiently "solving" low-rank positive semidefinite correlation clustering by employing a procedure for zonotope vertex enumeration. We demonstrate the effectiveness and speed of our algorithm by using it to solve several clustering problems on both synthetic and real-world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge