Suboptimality bounds for trace-bounded SDPs enable a faster and scalable low-rank SDP solver SDPLR+

Semidefinite programs (SDPs) and their solvers are powerful tools with many applications in machine learning and data science. Designing scalable SDP solvers is challenging because by standard the positive semidefinite decision variable is an $n \times n$ dense matrix, even though the input is often an $n \times n$ sparse matrix. However, the information in the solution may not correspond to a full-rank dense matrix as shown by Bavinok and Pataki. Two decades ago, Burer and Monterio developed an SDP solver $\texttt{SDPLR}$ that optimizes over a low-rank factorization instead of the full matrix. This greatly decreases the storage cost and works well for many problems. The original solver $\texttt{SDPLR}$ tracks only the primal infeasibility of the solution, limiting the technique's flexibility to produce moderate accuracy solutions. We use a suboptimality bound for trace-bounded SDP problems that enables us to track the progress better and perform early termination. We then develop $\texttt{SDPLR+}$, which starts the optimization with an extremely low-rank factorization and dynamically updates the rank based on the primal infeasibility and suboptimality. This further speeds up the computation and saves the storage cost. Numerical experiments on Max Cut, Minimum Bisection, Cut Norm, and Lov\'{a}sz Theta problems with many recent memory-efficient scalable SDP solvers demonstrate its scalability up to problems with million-by-million decision variables and it is often the fastest solver to a moderate accuracy of $10^{-2}$.

Topological structure of complex predictions

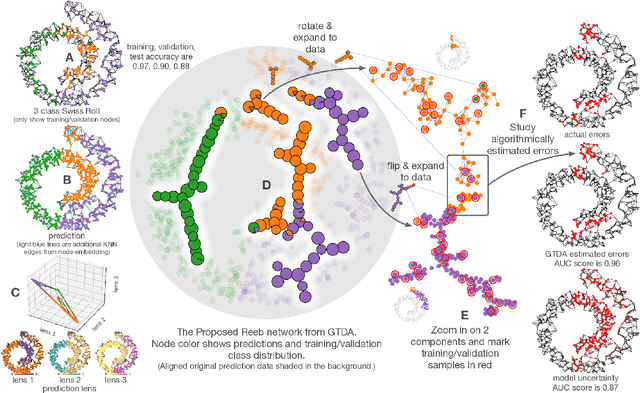
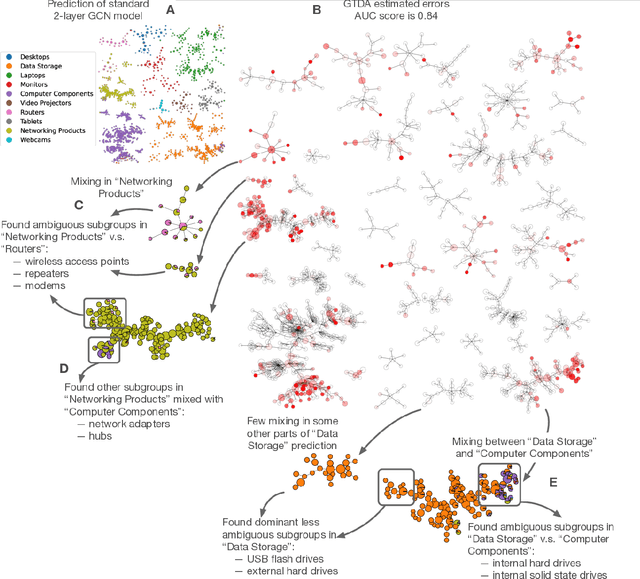
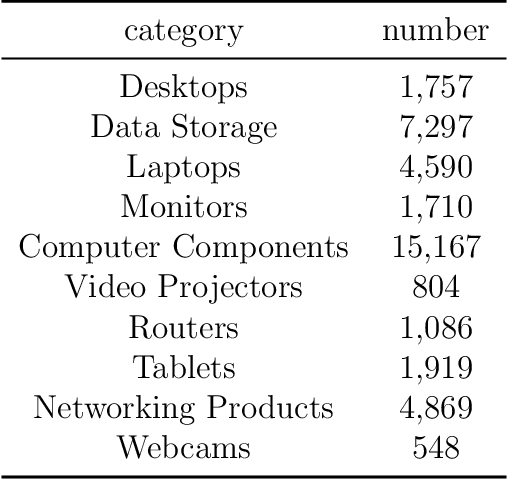
Complex prediction models such as deep learning are the output from fitting machine learning, neural networks, or AI models to a set of training data. These are now standard tools in science. A key challenge with the current generation of models is that they are highly parameterized, which makes describing and interpreting the prediction strategies difficult. We use topological data analysis to transform these complex prediction models into pictures representing a topological view. The result is a map of the predictions that enables inspection. The methods scale up to large datasets across different domains and enable us to detect labeling errors in training data, understand generalization in image classification, and inspect predictions of likely pathogenic mutations in the BRCA1 gene.

A flexible PageRank-based graph embedding framework closely related to spectral eigenvector embeddings

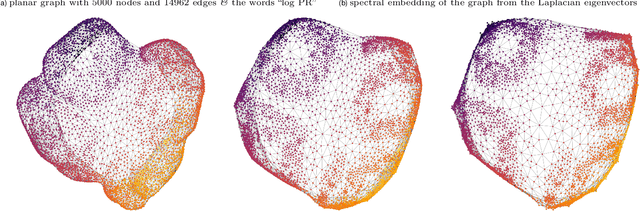
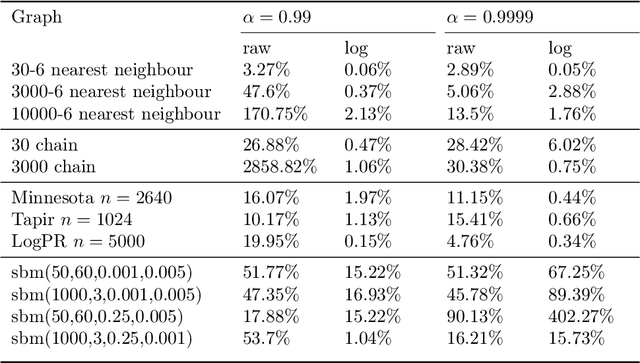
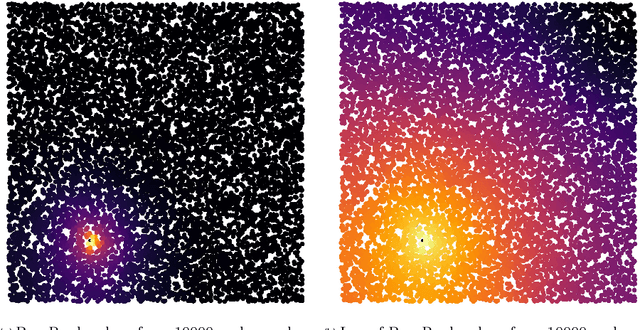
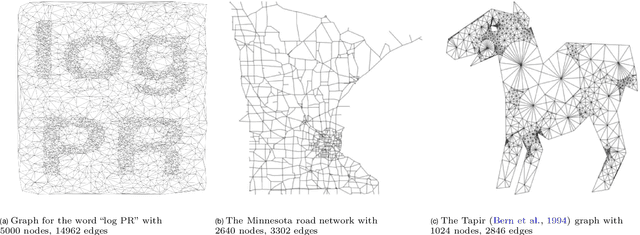
We study a simple embedding technique based on a matrix of personalized PageRank vectors seeded on a random set of nodes. We show that the embedding produced by the element-wise logarithm of this matrix (1) are related to the spectral embedding for a class of graphs where spectral embeddings are significant, and hence useful representation of the data, (2) can be done for the entire network or a smaller part of it, which enables precise local representation, and (3) uses a relatively small number of PageRank vectors compared to the size of the networks. Most importantly, the general nature of this embedding strategy opens up many emerging applications, where eigenvector and spectral techniques may not be well established, to the PageRank-based relatives. For instance, similar techniques can be used on PageRank vectors from hypergraphs to get "spectral-like" embeddings.

Strongly local p-norm-cut algorithms for semi-supervised learning and local graph clustering

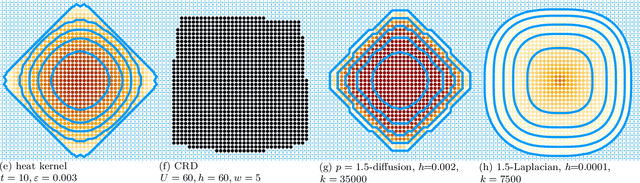
Graph based semi-supervised learning is the problem of learning a labeling function for the graph nodes given a few example nodes, often called seeds, usually under the assumption that the graph's edges indicate similarity of labels. This is closely related to the local graph clustering or community detection problem of finding a cluster or community of nodes around a given seed. For this problem, we propose a novel generalization of random walk, diffusion, or smooth function methods in the literature to a convex p-norm cut function. The need for our p-norm methods is that, in our study of existing methods, we find those principled methods based on eigenvector, spectral, random walk, or linear system often have difficulty capturing the correct boundary of a target label or target cluster. In contrast, 1-norm or maxflow-mincut based methods capture the boundary, but cannot grow from small seed set; hybrid procedures that use both have many hard to set parameters. In this paper, we propose a generalization of the objective function behind these methods involving p-norms. To solve the p-norm cut problem we give a strongly local algorithm -- one whose runtime depends on the size of the output rather than the size of the graph. Our method can be thought as a nonlinear generalization of the Anderson-Chung-Lang push procedure to approximate a personalized PageRank vector efficiently. Our procedure is general and can solve other types of nonlinear objective functions, such as p-norm variants of Huber losses. We provide a theoretical analysis of finding planted target clusters with our method and show that the p-norm cut functions improve on the standard Cheeger inequalities for random walk and spectral methods. Finally, we demonstrate the speed and accuracy of our new method in synthetic and real world datasets. Our code is available.

Parameterized Objectives and Algorithms for Clustering Bipartite Graphs and Hypergraphs

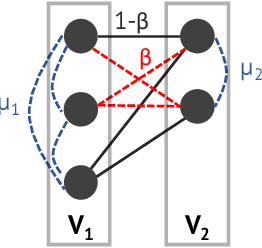
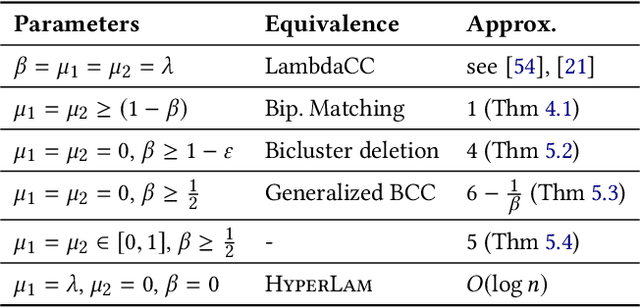
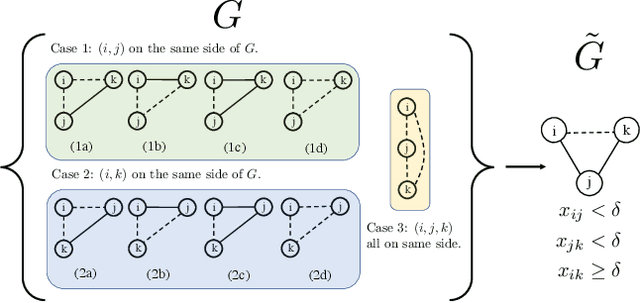
Graph clustering objective functions with tunable resolution parameters make it possible to detect different types of clustering structure in the same graph. These objectives also provide a unifying view of other non-parametric objectives, which often can be captured as special cases. Previous research has largely focused on parametric objectives for standard graphs, in which all nodes are of the same type, and edges model pairwise relationships. In our work, we introduced parameterized objective functions and approximation algorithms specifically for clustering bipartite graphs and hypergraphs, based on correlation clustering. This enables us to develop principled approaches for clustering datasets with different node types (bipartite graphs) or multiway relationships (hypergraphs). Our hypergraph objective is related to higher-order notions of modularity and normalized cut, and is amenable to approximation algorithms via hypergraph expansion techniques. Our bipartite objective generalizes standard bipartite correlation clustering, and in a certain parameter regime is equivalent to bicluster deletion, i.e., removing a minimum number of edges to separate a bipartite graph into disjoint bicliques. The problem in general is NP-hard, but we show that in a certain parameter regime it is equivalent to a bipartite matching problem, meaning that it is polynomial time solvable in this regime. For other regimes, we provide approximation guarantees based on LP-rounding. Our results include the first constant factor approximation algorithm for bicluster deletion. We illustrate the flexibility of our framework in several experiments. This includes clustering a food web and an email network based on higher-order motif structure, detecting clusters of retail products in product review hypergraph, and evaluating our algorithms across a range of parameter settings on several real world bipartite graphs.

Learning Resolution Parameters for Graph Clustering

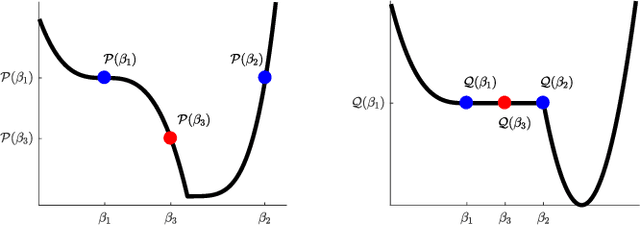
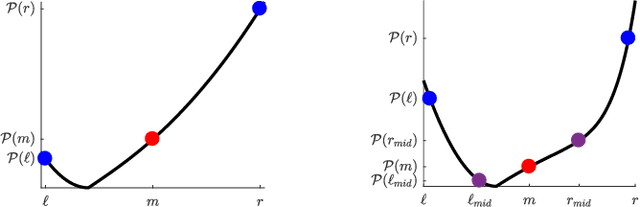
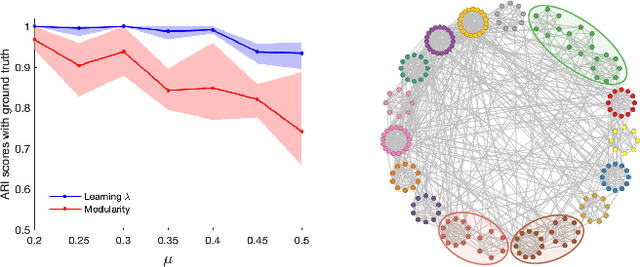
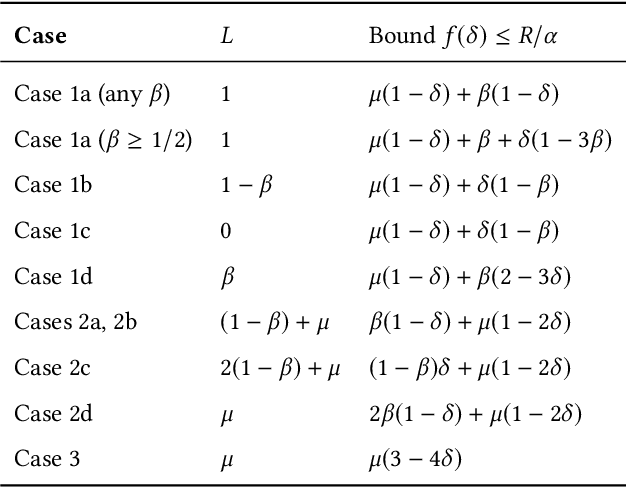
Finding clusters of well-connected nodes in a graph is an extensively studied problem in graph-based data analysis. Because of its many applications, a large number of distinct graph clustering objective functions and algorithms have already been proposed and analyzed. To aid practitioners in determining the best clustering approach to use in different applications, we present new techniques for automatically learning how to set clustering resolution parameters. These parameters control the size and structure of communities that are formed by optimizing a generalized objective function. We begin by formalizing the notion of a parameter fitness function, which measures how well a fixed input clustering approximately solves a generalized clustering objective for a specific resolution parameter value. Under reasonable assumptions, which suit two key graph clustering applications, such a parameter fitness function can be efficiently minimized using a bisection-like method, yielding a resolution parameter that fits well with the example clustering. We view our framework as a type of single-shot hyperparameter tuning, as we are able to learn a good resolution parameter with just a single example. Our general approach can be applied to learn resolution parameters for both local and global graph clustering objectives. We demonstrate its utility in several experiments on real-world data where it is helpful to learn resolution parameters from a given example clustering.

A Parallel Projection Method for Metric Constrained Optimization

Many clustering applications in machine learning and data mining rely on solving metric-constrained optimization problems. These problems are characterized by $O(n^3)$ constraints that enforce triangle inequalities on distance variables associated with $n$ objects in a large dataset. Despite its usefulness, metric-constrained optimization is challenging in practice due to the cubic number of constraints and the high-memory requirements of standard optimization software. Recent work has shown that iterative projection methods are able to solve metric-constrained optimization problems on a much larger scale than was previously possible, thanks to their comparatively low memory requirement. However, the major limitation of projection methods is their slow convergence rate. In this paper we present a parallel projection method for metric-constrained optimization which allows us to speed up the convergence rate in practice. The key to our approach is a new parallel execution schedule that allows us to perform projections at multiple metric constraints simultaneously without any conflicts or locking of variables. We illustrate the effectiveness of this execution schedule by implementing and testing a parallel projection method for solving the metric-constrained linear programming relaxation of correlation clustering. We show numerous experimental results on problems involving up to 2.9 trillion constraints.

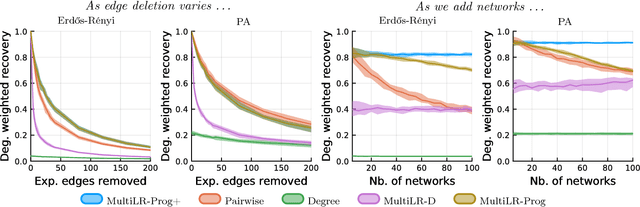
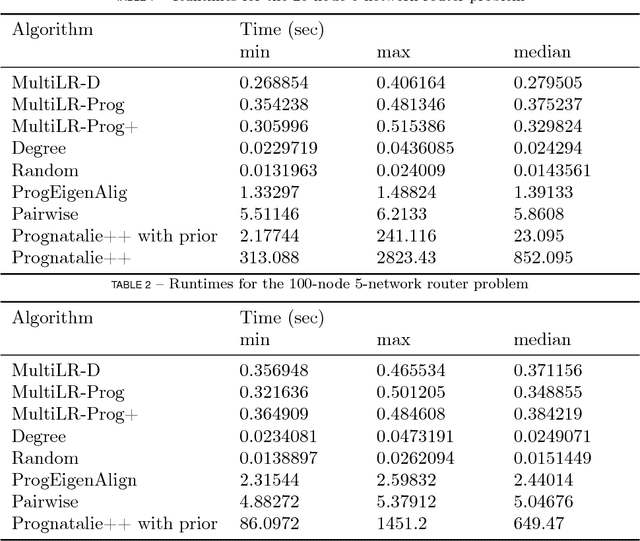
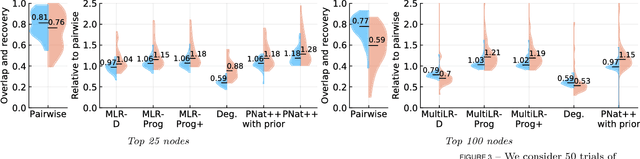
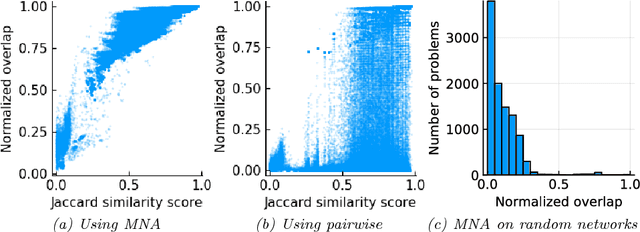
Low rank methods for multiple network alignment

Multiple network alignment is the problem of identifying similar and related regions in a given set of networks. While there are a large number of effective techniques for pairwise problems with two networks that scale in terms of edges, these cannot be readily extended to align multiple networks as the computational complexity will tend to grow exponentially with the number of networks.In this paper we introduce a new multiple network alignment algorithm and framework that is effective at aligning thousands of networks with thousands of nodes. The key enabling technique of our algorithm is identifying an exact and easy to compute low-rank tensor structure inside of a principled heuristic procedure for pairwise network alignment called IsoRank. This can be combined with a new algorithm for $k$-dimensional matching problems on low-rank tensors to produce the alignment. We demonstrate results on synthetic and real-world problems that show our technique (i) is as good or better in terms of quality as existing methods, when they work on small problems, while running considerably faster and (ii) is able to scale to aligning a number of networks unreachable by current methods. We show in this paper that our method is the realistic choice for aligning multiple networks when no prior information is present.

Correlation Clustering with Low-Rank Matrices

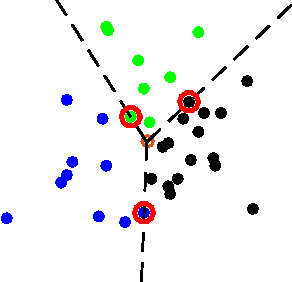
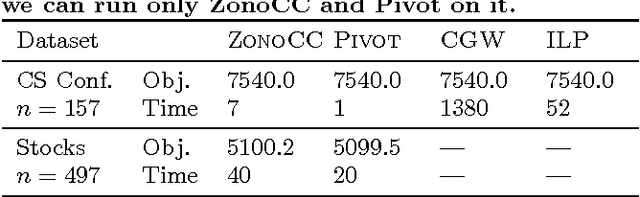
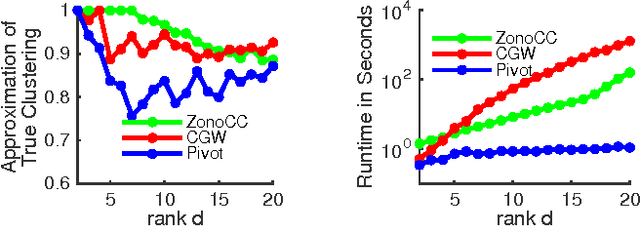
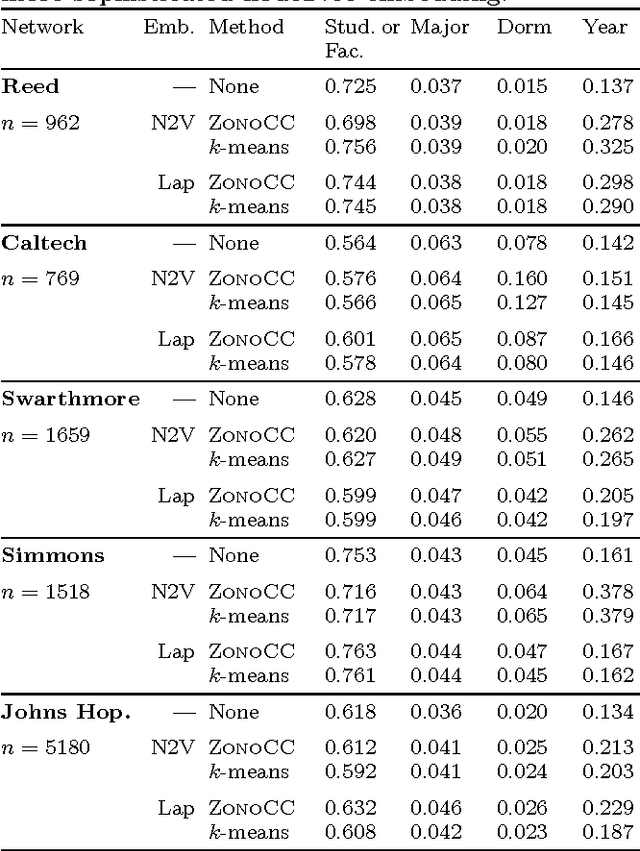
Correlation clustering is a technique for aggregating data based on qualitative information about which pairs of objects are labeled 'similar' or 'dissimilar.' Because the optimization problem is NP-hard, much of the previous literature focuses on finding approximation algorithms. In this paper we explore how to solve the correlation clustering objective exactly when the data to be clustered can be represented by a low-rank matrix. We prove in particular that correlation clustering can be solved in polynomial time when the underlying matrix is positive semidefinite with small constant rank, but that the task remains NP-hard in the presence of even one negative eigenvalue. Based on our theoretical results, we develop an algorithm for efficiently "solving" low-rank positive semidefinite correlation clustering by employing a procedure for zonotope vertex enumeration. We demonstrate the effectiveness and speed of our algorithm by using it to solve several clustering problems on both synthetic and real-world data.

Multi-way Monte Carlo Method for Linear Systems

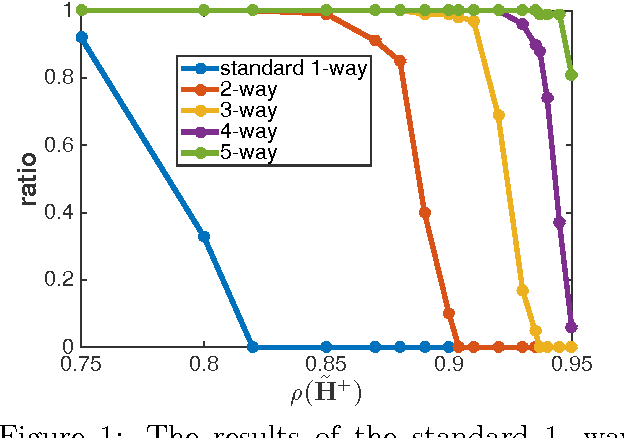
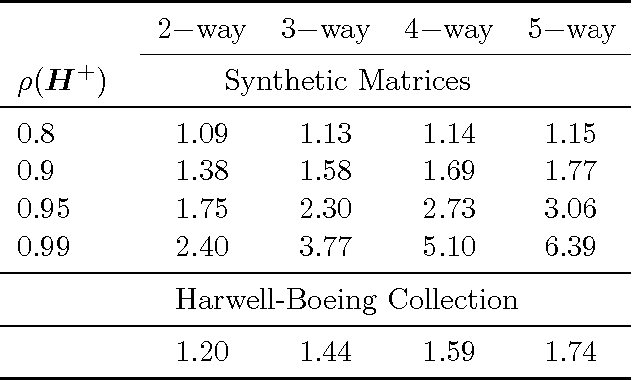
We study the Monte Carlo method for solving a linear system of the form $x = H x + b$. A sufficient condition for the method to work is $\| H \| < 1$, which greatly limits the usability of this method. We improve this condition by proposing a new multi-way Markov random walk, which is a generalization of the standard Markov random walk. Under our new framework we prove that the necessary and sufficient condition for our method to work is the spectral radius $\rho(H^{+}) < 1$, which is a weaker requirement than $\| H \| < 1$. In addition to solving more problems, our new method can work faster than the standard algorithm. In numerical experiments on both synthetic and real world matrices, we demonstrate the effectiveness of our new method.