Addressing Computational Bottlenecks in Higher-Order Graph Matching with Tensor Kronecker Product Structure

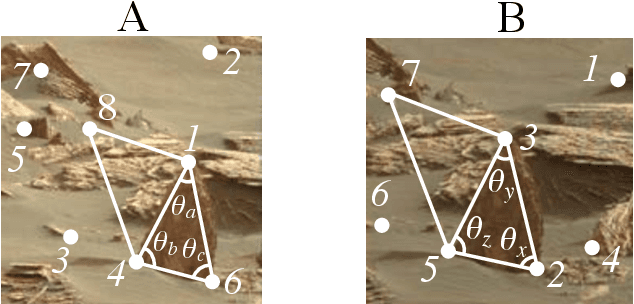
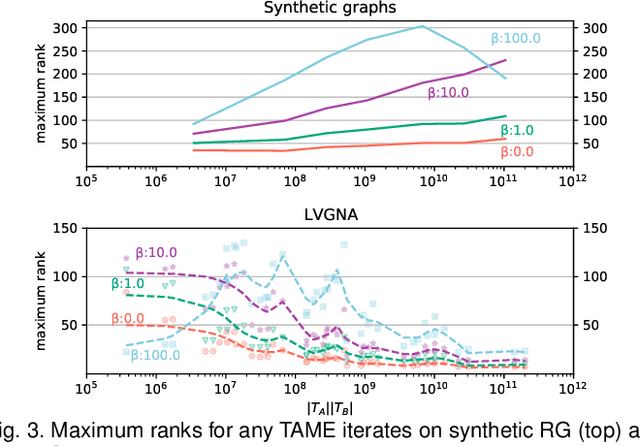
Graph matching, also known as network alignment, is the problem of finding a correspondence between the vertices of two separate graphs with strong applications in image correspondence and functional inference in protein networks. One class of successful techniques is based on tensor Kronecker products and tensor eigenvectors. A challenge with these techniques are memory and computational demands that are quadratic (or worse) in terms of problem size. In this manuscript we present and apply a theory of tensor Kronecker products to tensor based graph alignment algorithms to reduce their runtime complexity from quadratic to linear with no appreciable loss of quality. In terms of theory, we show that many matrix Kronecker product identities generalize to straightforward tensor counterparts, which is rare in tensor literature. Improved computation codes for two existing algorithms that utilize this new theory achieve a minimum 10 fold runtime improvement.

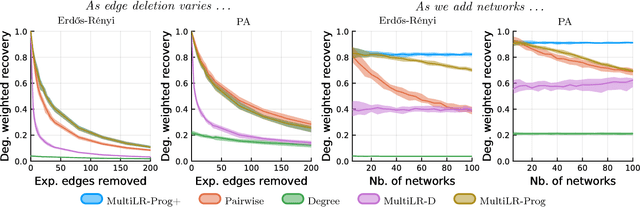
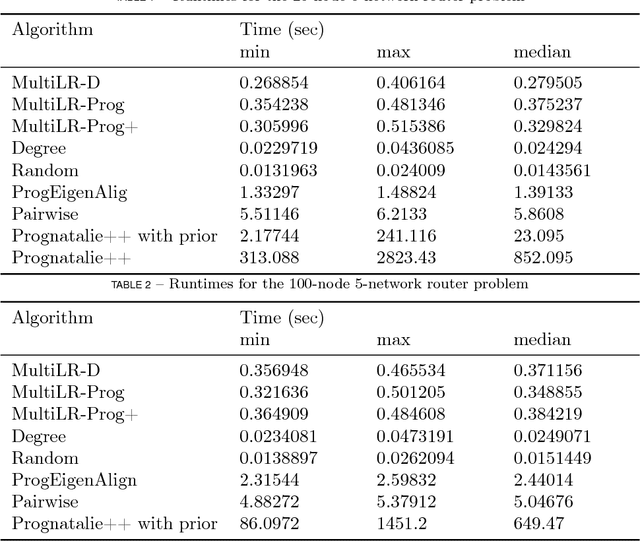
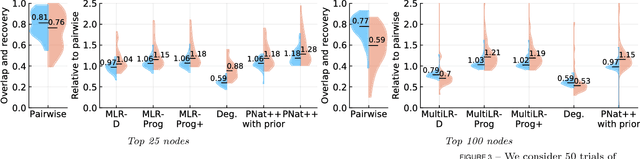
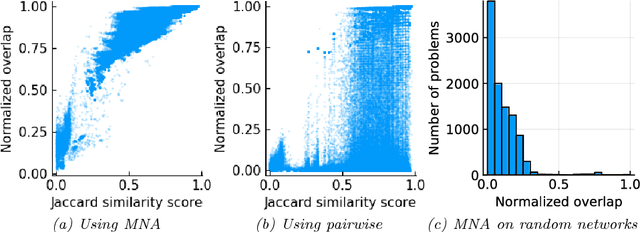
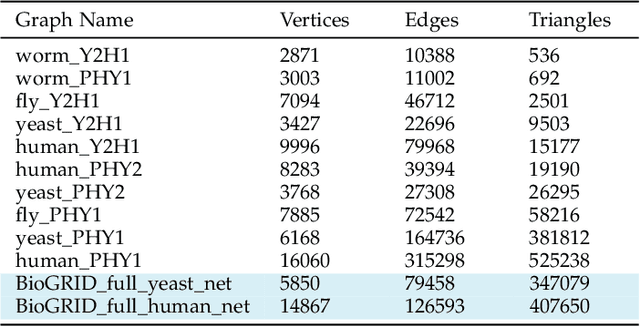
Low rank methods for multiple network alignment

Multiple network alignment is the problem of identifying similar and related regions in a given set of networks. While there are a large number of effective techniques for pairwise problems with two networks that scale in terms of edges, these cannot be readily extended to align multiple networks as the computational complexity will tend to grow exponentially with the number of networks.In this paper we introduce a new multiple network alignment algorithm and framework that is effective at aligning thousands of networks with thousands of nodes. The key enabling technique of our algorithm is identifying an exact and easy to compute low-rank tensor structure inside of a principled heuristic procedure for pairwise network alignment called IsoRank. This can be combined with a new algorithm for $k$-dimensional matching problems on low-rank tensors to produce the alignment. We demonstrate results on synthetic and real-world problems that show our technique (i) is as good or better in terms of quality as existing methods, when they work on small problems, while running considerably faster and (ii) is able to scale to aligning a number of networks unreachable by current methods. We show in this paper that our method is the realistic choice for aligning multiple networks when no prior information is present.