Addressing Computational Bottlenecks in Higher-Order Graph Matching with Tensor Kronecker Product Structure

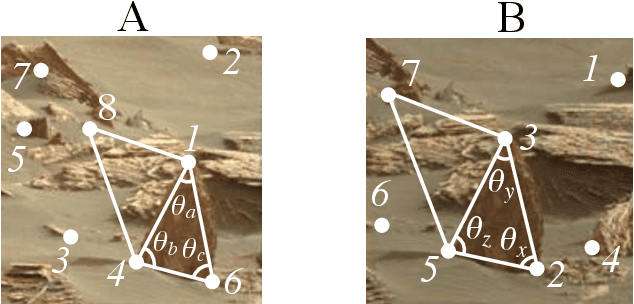
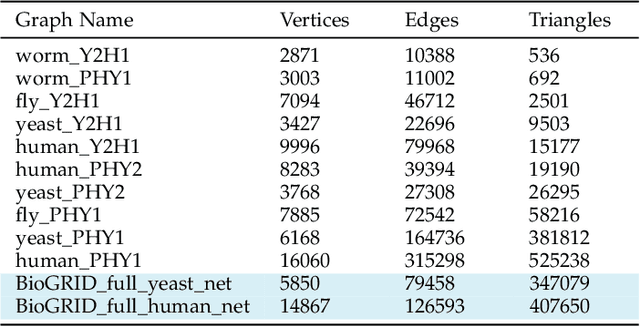
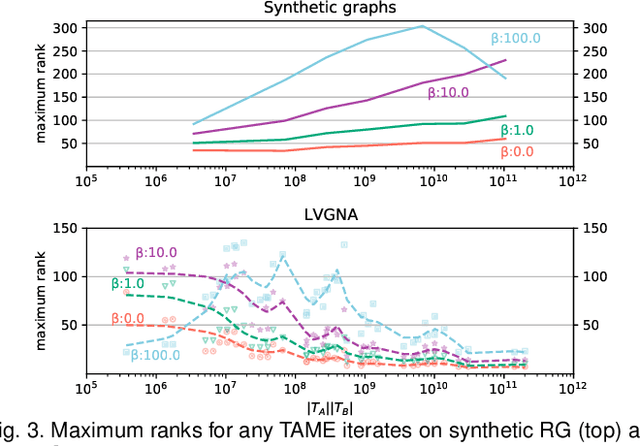
Graph matching, also known as network alignment, is the problem of finding a correspondence between the vertices of two separate graphs with strong applications in image correspondence and functional inference in protein networks. One class of successful techniques is based on tensor Kronecker products and tensor eigenvectors. A challenge with these techniques are memory and computational demands that are quadratic (or worse) in terms of problem size. In this manuscript we present and apply a theory of tensor Kronecker products to tensor based graph alignment algorithms to reduce their runtime complexity from quadratic to linear with no appreciable loss of quality. In terms of theory, we show that many matrix Kronecker product identities generalize to straightforward tensor counterparts, which is rare in tensor literature. Improved computation codes for two existing algorithms that utilize this new theory achieve a minimum 10 fold runtime improvement.

A Projection Method for Metric-Constrained Optimization

We outline a new approach for solving optimization problems which enforce triangle inequalities on output variables. We refer to this as metric-constrained optimization, and give several examples where problems of this form arise in machine learning applications and theoretical approximation algorithms for graph clustering. Although these problem are interesting from a theoretical perspective, they are challenging to solve in practice due to the high memory requirement of black-box solvers. In order to address this challenge we first prove that the metric-constrained linear program relaxation of correlation clustering is equivalent to a special case of the metric nearness problem. We then developed a general solver for metric-constrained linear and quadratic programs by generalizing and improving a simple projection algorithm originally developed for metric nearness. We give several novel approximation guarantees for using our framework to find lower bounds for optimal solutions to several challenging graph clustering problems. We also demonstrate the power of our framework by solving optimizing problems involving up to 10^{8} variables and 10^{11} constraints.

Retrospective Higher-Order Markov Processes for User Trails

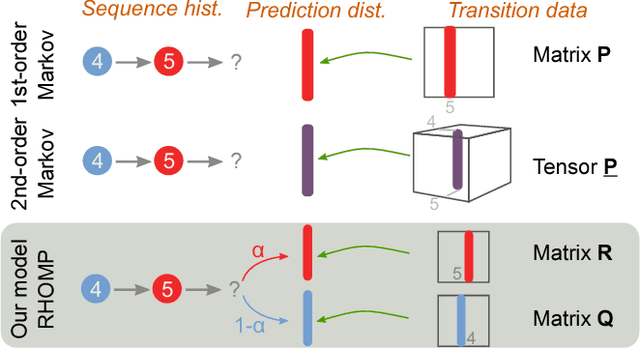
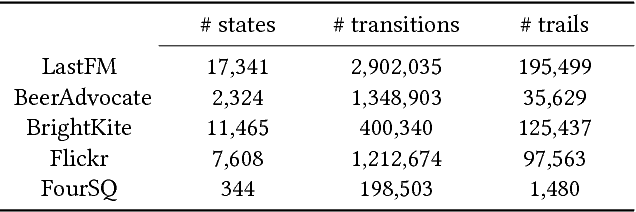
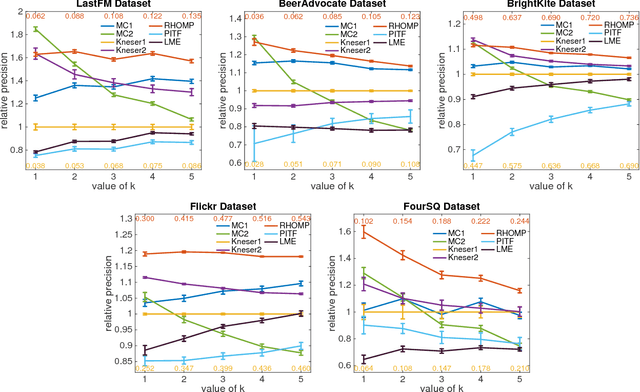
Users form information trails as they browse the web, checkin with a geolocation, rate items, or consume media. A common problem is to predict what a user might do next for the purposes of guidance, recommendation, or prefetching. First-order and higher-order Markov chains have been widely used methods to study such sequences of data. First-order Markov chains are easy to estimate, but lack accuracy when history matters. Higher-order Markov chains, in contrast, have too many parameters and suffer from overfitting the training data. Fitting these parameters with regularization and smoothing only offers mild improvements. In this paper we propose the retrospective higher-order Markov process (RHOMP) as a low-parameter model for such sequences. This model is a special case of a higher-order Markov chain where the transitions depend retrospectively on a single history state instead of an arbitrary combination of history states. There are two immediate computational advantages: the number of parameters is linear in the order of the Markov chain and the model can be fit to large state spaces. Furthermore, by providing a specific structure to the higher-order chain, RHOMPs improve the model accuracy by efficiently utilizing history states without risks of overfitting the data. We demonstrate how to estimate a RHOMP from data and we demonstrate the effectiveness of our method on various real application datasets spanning geolocation data, review sequences, and business locations. The RHOMP model uniformly outperforms higher-order Markov chains, Kneser-Ney regularization, and tensor factorizations in terms of prediction accuracy.