Multi-way Monte Carlo Method for Linear Systems
Paper and Code
Aug 15, 2016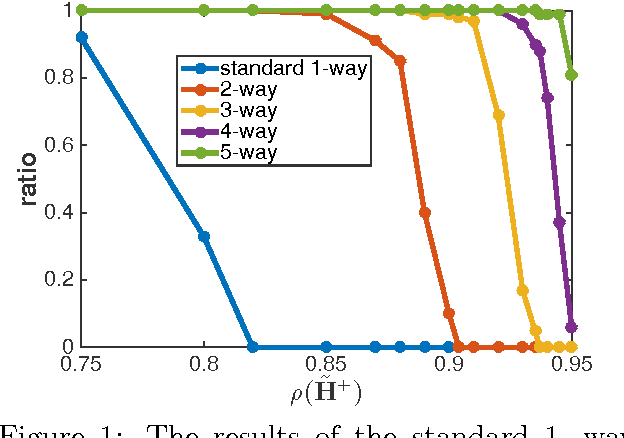
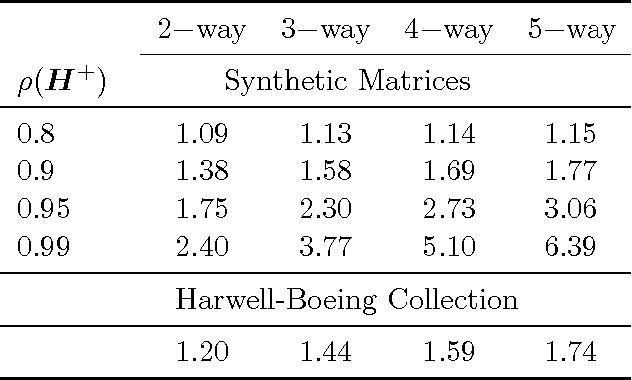
We study the Monte Carlo method for solving a linear system of the form $x = H x + b$. A sufficient condition for the method to work is $\| H \| < 1$, which greatly limits the usability of this method. We improve this condition by proposing a new multi-way Markov random walk, which is a generalization of the standard Markov random walk. Under our new framework we prove that the necessary and sufficient condition for our method to work is the spectral radius $\rho(H^{+}) < 1$, which is a weaker requirement than $\| H \| < 1$. In addition to solving more problems, our new method can work faster than the standard algorithm. In numerical experiments on both synthetic and real world matrices, we demonstrate the effectiveness of our new method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge