Fast Debiasing of the LASSO Estimator
Paper and Code
Feb 27, 2025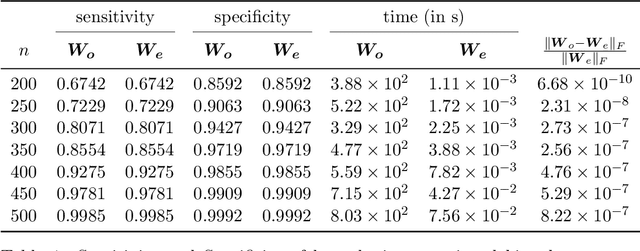
In high-dimensional sparse regression, the \textsc{Lasso} estimator offers excellent theoretical guarantees but is well-known to produce biased estimates. To address this, \cite{Javanmard2014} introduced a method to ``debias" the \textsc{Lasso} estimates for a random sub-Gaussian sensing matrix $\boldsymbol{A}$. Their approach relies on computing an ``approximate inverse" $\boldsymbol{M}$ of the matrix $\boldsymbol{A}^\top \boldsymbol{A}/n$ by solving a convex optimization problem. This matrix $\boldsymbol{M}$ plays a critical role in mitigating bias and allowing for construction of confidence intervals using the debiased \textsc{Lasso} estimates. However the computation of $\boldsymbol{M}$ is expensive in practice as it requires iterative optimization. In the presented work, we re-parameterize the optimization problem to compute a ``debiasing matrix" $\boldsymbol{W} := \boldsymbol{AM}^{\top}$ directly, rather than the approximate inverse $\boldsymbol{M}$. This reformulation retains the theoretical guarantees of the debiased \textsc{Lasso} estimates, as they depend on the \emph{product} $\boldsymbol{AM}^{\top}$ rather than on $\boldsymbol{M}$ alone. Notably, we provide a simple, computationally efficient, closed-form solution for $\boldsymbol{W}$ under similar conditions for the sensing matrix $\boldsymbol{A}$ used in the original debiasing formulation, with an additional condition that the elements of every row of $\boldsymbol{A}$ have uncorrelated entries. Also, the optimization problem based on $\boldsymbol{W}$ guarantees a unique optimal solution, unlike the original formulation based on $\boldsymbol{M}$. We verify our main result with numerical simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge