Machine Learning for Scent: Learning Generalizable Perceptual Representations of Small Molecules

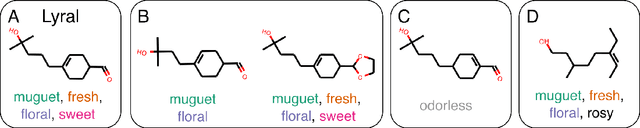
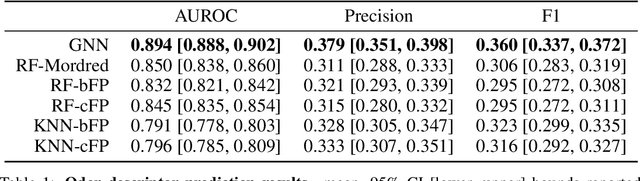
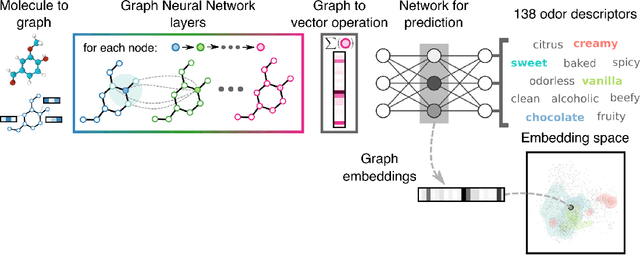
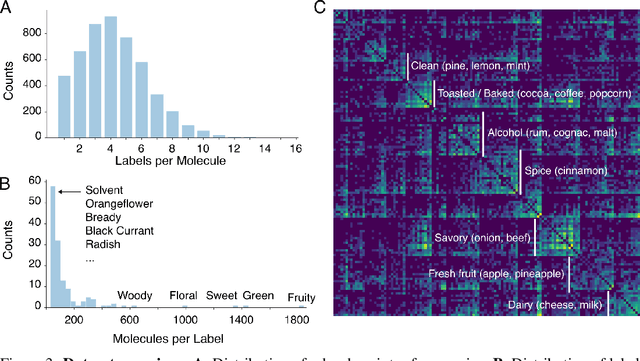
Predicting the relationship between a molecule's structure and its odor remains a difficult, decades-old task. This problem, termed quantitative structure-odor relationship (QSOR) modeling, is an important challenge in chemistry, impacting human nutrition, manufacture of synthetic fragrance, the environment, and sensory neuroscience. We propose the use of graph neural networks for QSOR, and show they significantly out-perform prior methods on a novel data set labeled by olfactory experts. Additional analysis shows that the learned embeddings from graph neural networks capture a meaningful odor space representation of the underlying relationship between structure and odor, as demonstrated by strong performance on two challenging transfer learning tasks. Machine learning has already had a large impact on the senses of sight and sound. Based on these early results with graph neural networks for molecular properties, we hope machine learning can eventually do for olfaction what it has already done for vision and hearing.

Tangent: Automatic Differentiation Using Source Code Transformation in Python

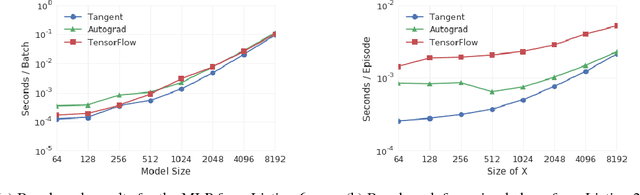
Automatic differentiation (AD) is an essential primitive for machine learning programming systems. Tangent is a new library that performs AD using source code transformation (SCT) in Python. It takes numeric functions written in a syntactic subset of Python and NumPy as input, and generates new Python functions which calculate a derivative. This approach to automatic differentiation is different from existing packages popular in machine learning, such as TensorFlow and Autograd. Advantages are that Tangent generates gradient code in Python which is readable by the user, easy to understand and debug, and has no runtime overhead. Tangent also introduces abstractions for easily injecting logic into the generated gradient code, further improving usability.

Composing graphical models with neural networks for structured representations and fast inference

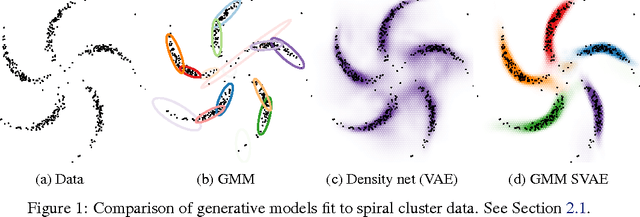
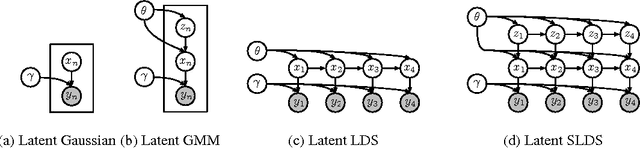
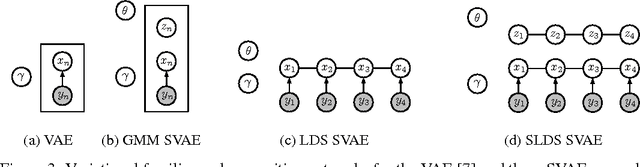
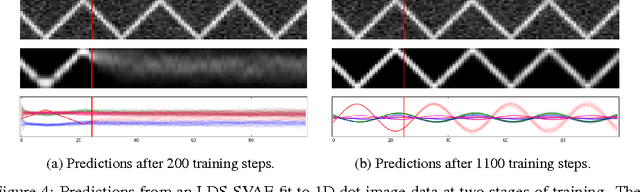
We propose a general modeling and inference framework that composes probabilistic graphical models with deep learning methods and combines their respective strengths. Our model family augments graphical structure in latent variables with neural network observation models. For inference, we extend variational autoencoders to use graphical model approximating distributions with recognition networks that output conjugate potentials. All components of these models are learned simultaneously with a single objective, giving a scalable algorithm that leverages stochastic variational inference, natural gradients, graphical model message passing, and the reparameterization trick. We illustrate this framework with several example models and an application to mouse behavioral phenotyping.