A New Class of Upper Bounds on the Log Partition Function

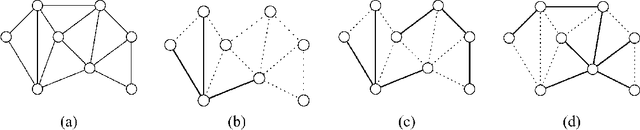
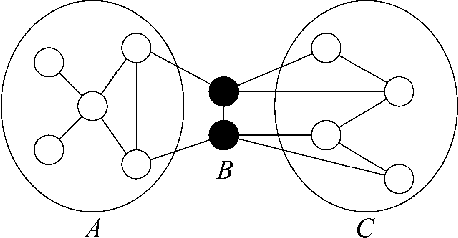
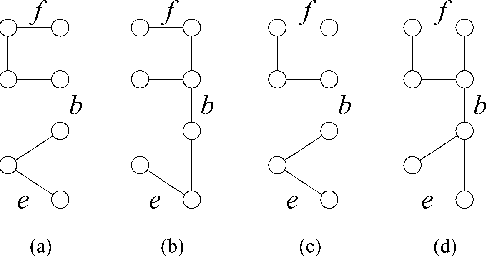
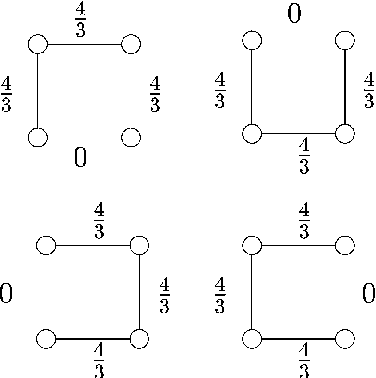
Bounds on the log partition function are important in a variety of contexts, including approximate inference, model fitting, decision theory, and large deviations analysis. We introduce a new class of upper bounds on the log partition function, based on convex combinations of distributions in the exponential domain, that is applicable to an arbitrary undirected graphical model. In the special case of convex combinations of tree-structured distributions, we obtain a family of variational problems, similar to the Bethe free energy, but distinguished by the following desirable properties: i. they are cnvex, and have a unique global minimum; and ii. the global minimum gives an upper bound on the log partition function. The global minimum is defined by stationary conditions very similar to those defining fixed points of belief propagation or tree-based reparameterization Wainwright et al., 2001. As with BP fixed points, the elements of the minimizing argument can be used as approximations to the marginals of the original model. The analysis described here can be extended to structures of higher treewidth e.g., hypertrees, thereby making connections with more advanced approximations e.g., Kikuchi and variants Yedidia et al., 2001; Minka, 2001.