Dual Averaging for Distributed Optimization: Convergence Analysis and Network Scaling
Paper and Code
Apr 10, 2011
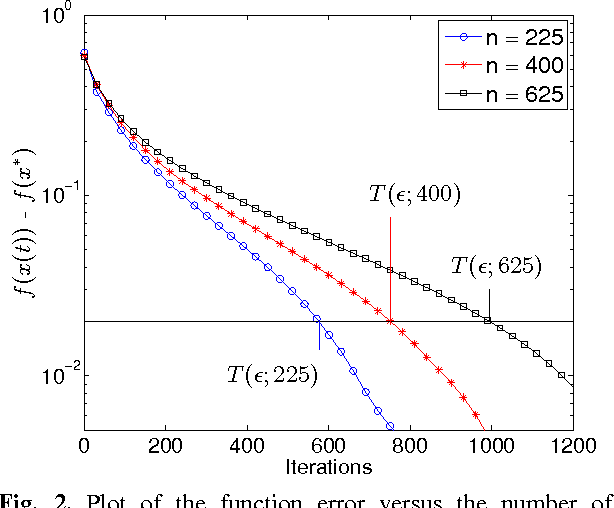
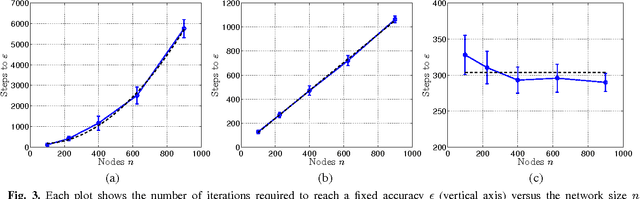

The goal of decentralized optimization over a network is to optimize a global objective formed by a sum of local (possibly nonsmooth) convex functions using only local computation and communication. It arises in various application domains, including distributed tracking and localization, multi-agent co-ordination, estimation in sensor networks, and large-scale optimization in machine learning. We develop and analyze distributed algorithms based on dual averaging of subgradients, and we provide sharp bounds on their convergence rates as a function of the network size and topology. Our method of analysis allows for a clear separation between the convergence of the optimization algorithm itself and the effects of communication constraints arising from the network structure. In particular, we show that the number of iterations required by our algorithm scales inversely in the spectral gap of the network. The sharpness of this prediction is confirmed both by theoretical lower bounds and simulations for various networks. Our approach includes both the cases of deterministic optimization and communication, as well as problems with stochastic optimization and/or communication.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge