When is it Better to Compare than to Score?
Paper and Code
Jun 25, 2014

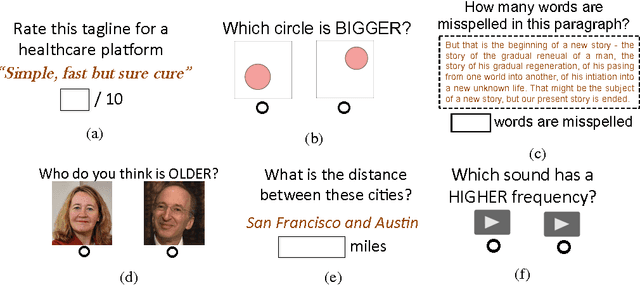

When eliciting judgements from humans for an unknown quantity, one often has the choice of making direct-scoring (cardinal) or comparative (ordinal) measurements. In this paper we study the relative merits of either choice, providing empirical and theoretical guidelines for the selection of a measurement scheme. We provide empirical evidence based on experiments on Amazon Mechanical Turk that in a variety of tasks, (pairwise-comparative) ordinal measurements have lower per sample noise and are typically faster to elicit than cardinal ones. Ordinal measurements however typically provide less information. We then consider the popular Thurstone and Bradley-Terry-Luce (BTL) models for ordinal measurements and characterize the minimax error rates for estimating the unknown quantity. We compare these minimax error rates to those under cardinal measurement models and quantify for what noise levels ordinal measurements are better. Finally, we revisit the data collected from our experiments and show that fitting these models confirms this prediction: for tasks where the noise in ordinal measurements is sufficiently low, the ordinal approach results in smaller errors in the estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge