Toward the Fundamental Limits of Imitation Learning
Paper and Code
Sep 13, 2020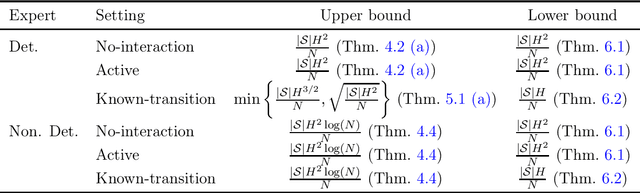
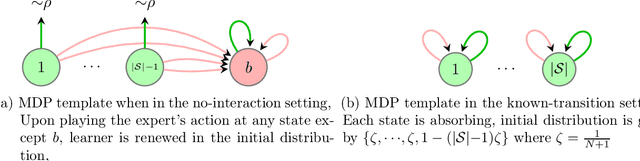


Imitation learning (IL) aims to mimic the behavior of an expert policy in a sequential decision-making problem given only demonstrations. In this paper, we focus on understanding the minimax statistical limits of IL in episodic Markov Decision Processes (MDPs). We first consider the setting where the learner is provided a dataset of $N$ expert trajectories ahead of time, and cannot interact with the MDP. Here, we show that the policy which mimics the expert whenever possible is in expectation $\lesssim \frac{|\mathcal{S}| H^2 \log (N)}{N}$ suboptimal compared to the value of the expert, even when the expert follows an arbitrary stochastic policy. Here $\mathcal{S}$ is the state space, and $H$ is the length of the episode. Furthermore, we establish a suboptimality lower bound of $\gtrsim |\mathcal{S}| H^2 / N$ which applies even if the expert is constrained to be deterministic, or if the learner is allowed to actively query the expert at visited states while interacting with the MDP for $N$ episodes. To our knowledge, this is the first algorithm with suboptimality having no dependence on the number of actions, under no additional assumptions. We then propose a novel algorithm based on minimum-distance functionals in the setting where the transition model is given and the expert is deterministic. The algorithm is suboptimal by $\lesssim \min \{ H \sqrt{|\mathcal{S}| / N} ,\ |\mathcal{S}| H^{3/2} / N \}$, showing that knowledge of transition improves the minimax rate by at least a $\sqrt{H}$ factor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge