Grooming a Single Bandit Arm
Paper and Code
Jun 11, 2020
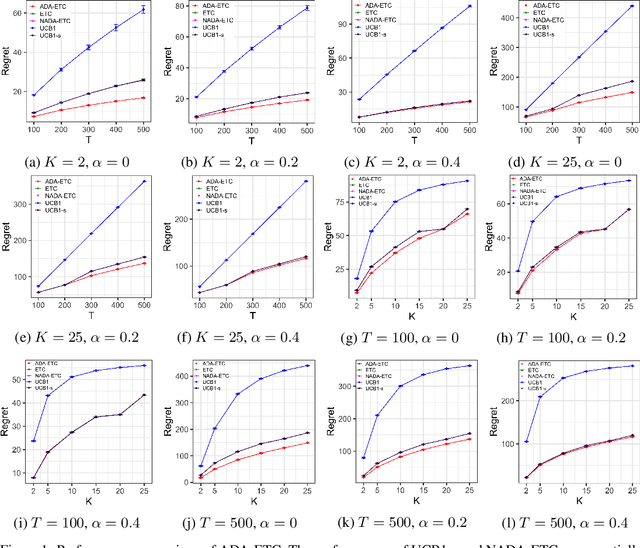
The stochastic multi-armed bandit problem captures the fundamental exploration vs. exploitation tradeoff inherent in online decision-making in uncertain settings. However, in several applications, the traditional objective of maximizing the expected sum of rewards obtained can be inappropriate. Motivated by the problem of optimizing job assignments to groom novice workers with unknown trainability in labor platforms, we consider a new objective in the classical setup. Instead of maximizing the expected total reward from $T$ pulls, we consider the vector of cumulative rewards earned from each of the $K$ arms at the end of $T$ pulls, and aim to maximize the expected value of the $highest$ cumulative reward. This corresponds to the objective of grooming a single, highly skilled worker using a limited supply of training jobs. For this new objective, we show that any policy must incur a regret of $\Omega(K^{1/3}T^{2/3})$ in the worst case. We design an explore-then-commit policy featuring exploration based on finely tuned confidence bounds on the mean reward and an adaptive stopping criterion, which adapts to the problem difficulty and guarantees a regret of $O(K^{1/3}T^{2/3}\sqrt{\log K})$ in the worst case. Our numerical experiments demonstrate that this policy improves upon several natural candidate policies for this setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge