Comparative Performance of Collaborative Bandit Algorithms: Effect of Sparsity and Exploration Intensity

This paper offers a comprehensive analysis of collaborative bandit algorithms and provides a thorough comparison of their performance. Collaborative bandits aim to improve the performance of contextual bandits by introducing relationships between arms (or items), allowing effective propagation of information. Collaboration among arms allows the feedback obtained through a single user (item) to be shared across related users (items). Introducing collaboration also alleviates the cold user (item) problem, i.e., lack of historical information when a new user (item) arriving to the platform with no prior record of interactions. In the context of modeling the relationships between arms (items), there are two main approaches: Hard and soft clustering. We call approaches that model the relationship between arms in an \textit{absolute} manner as hard clustering, i.e., the relationship is binary. Soft clustering relaxes membership constraints, allowing \textit{fuzzy} assignment. Focusing on the latter, we provide extensive experiments on the state-of-the-art collaborative contextual bandit algorithms and investigate the effect of sparsity and how the exploration intensity acts as a correction mechanism. Our numerical experiments demonstrate that controlling for sparsity in collaboration improves data efficiency and performance as it better informs learning. Meanwhile, increasing the exploration intensity acts as a correction because it effectively reduces variance due to potentially misspecified relationships among users. We observe that this misspecification is further remedied by introducing latent factors, and thus, increasing the dimensionality of the bandit parameters.

Grooming a Single Bandit Arm

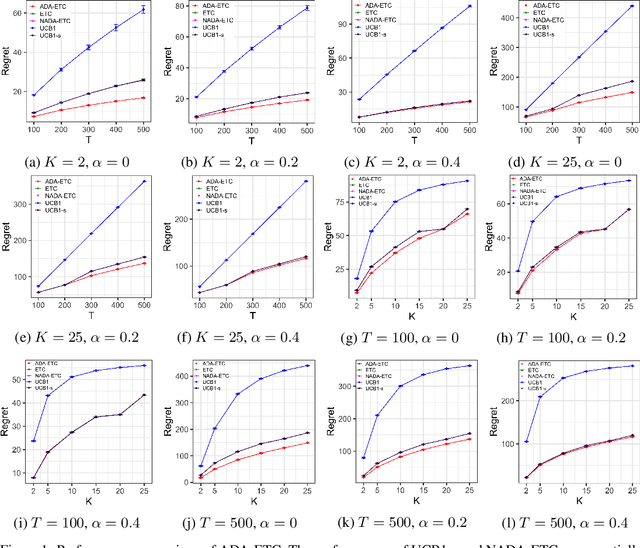
The stochastic multi-armed bandit problem captures the fundamental exploration vs. exploitation tradeoff inherent in online decision-making in uncertain settings. However, in several applications, the traditional objective of maximizing the expected sum of rewards obtained can be inappropriate. Motivated by the problem of optimizing job assignments to groom novice workers with unknown trainability in labor platforms, we consider a new objective in the classical setup. Instead of maximizing the expected total reward from $T$ pulls, we consider the vector of cumulative rewards earned from each of the $K$ arms at the end of $T$ pulls, and aim to maximize the expected value of the $highest$ cumulative reward. This corresponds to the objective of grooming a single, highly skilled worker using a limited supply of training jobs. For this new objective, we show that any policy must incur a regret of $\Omega(K^{1/3}T^{2/3})$ in the worst case. We design an explore-then-commit policy featuring exploration based on finely tuned confidence bounds on the mean reward and an adaptive stopping criterion, which adapts to the problem difficulty and guarantees a regret of $O(K^{1/3}T^{2/3}\sqrt{\log K})$ in the worst case. Our numerical experiments demonstrate that this policy improves upon several natural candidate policies for this setting.