Mixed-Integer Projections for Automated Data Correction of EMRs Improve Predictions of Sepsis among Hospitalized Patients

Machine learning (ML) models are increasingly pivotal in automating clinical decisions. Yet, a glaring oversight in prior research has been the lack of proper processing of Electronic Medical Record (EMR) data in the clinical context for errors and outliers. Addressing this oversight, we introduce an innovative projections-based method that seamlessly integrates clinical expertise as domain constraints, generating important meta-data that can be used in ML workflows. In particular, by using high-dimensional mixed-integer programs that capture physiological and biological constraints on patient vitals and lab values, we can harness the power of mathematical "projections" for the EMR data to correct patient data. Consequently, we measure the distance of corrected data from the constraints defining a healthy range of patient data, resulting in a unique predictive metric we term as "trust-scores". These scores provide insight into the patient's health status and significantly boost the performance of ML classifiers in real-life clinical settings. We validate the impact of our framework in the context of early detection of sepsis using ML. We show an AUROC of 0.865 and a precision of 0.922, that surpasses conventional ML models without such projections.

TACOS: Topology-Aware Collective Algorithm Synthesizer for Distributed Training

Collective communications are an indispensable part of distributed training. Running a topology-aware collective algorithm is crucial for optimizing communication performance by minimizing congestion. Today such algorithms only exist for a small set of simple topologies, limiting the topologies employed in training clusters and handling irregular topologies due to network failures. In this paper, we propose TACOS, an automated topology-aware collective synthesizer for arbitrary input network topologies. TACOS synthesized 3.73x faster All-Reduce algorithm over baselines, and synthesized collective algorithms for 512-NPU system in just 6.1 minutes.

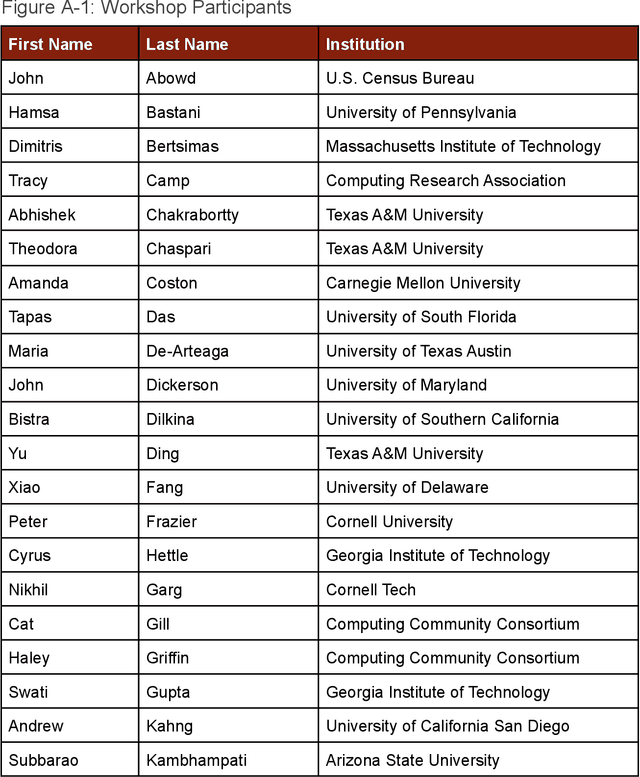
Artificial Intelligence/Operations Research Workshop 2 Report Out

This workshop Report Out focuses on the foundational elements of trustworthy AI and OR technology, and how to ensure all AI and OR systems implement these elements in their system designs. Four sessions on various topics within Trustworthy AI were held, these being Fairness, Explainable AI/Causality, Robustness/Privacy, and Human Alignment and Human-Computer Interaction. Following discussions of each of these topics, workshop participants also brainstormed challenge problems which require the collaboration of AI and OR researchers and will result in the integration of basic techniques from both fields to eventually benefit societal needs.

Tree DNN: A Deep Container Network

Multi-Task Learning (MTL) has shown its importance at user products for fast training, data efficiency, reduced overfitting etc. MTL achieves it by sharing the network parameters and training a network for multiple tasks simultaneously. However, MTL does not provide the solution, if each task needs training from a different dataset. In order to solve the stated problem, we have proposed an architecture named TreeDNN along with it's training methodology. TreeDNN helps in training the model with multiple datasets simultaneously, where each branch of the tree may need a different training dataset. We have shown in the results that TreeDNN provides competitive performance with the advantage of reduced ROM requirement for parameter storage and increased responsiveness of the system by loading only specific branch at inference time.

Reusing Combinatorial Structure: Faster Iterative Projections over Submodular Base Polytopes

Optimization algorithms such as projected Newton's method, FISTA, mirror descent and its variants enjoy near-optimal regret bounds and convergence rates, but suffer from a computational bottleneck of computing "projections'' in potentially each iteration (e.g., $O(T^{1/2})$ regret of online mirror descent). On the other hand, conditional gradient variants solve a linear optimization in each iteration, but result in suboptimal rates (e.g., $O(T^{3/4})$ regret of online Frank-Wolfe). Motivated by this trade-off in runtime v/s convergence rates, we consider iterative projections of close-by points over widely-prevalent submodular base polytopes $B(f)$. We develop a toolkit to speed up the computation of projections using both discrete and continuous perspectives. We subsequently adapt the away-step Frank-Wolfe algorithm to use this information and enable early termination. For the special case of cardinality based submodular polytopes, we improve the runtime of computing certain Bregman projections by a factor of $\Omega(n/\log(n))$. Our theoretical results show orders of magnitude reduction in runtime in preliminary computational experiments.

Taming Wild Price Fluctuations: Monotone Stochastic Convex Optimization with Bandit Feedback

Prices generated by automated price experimentation algorithms often display wild fluctuations, leading to unfavorable customer perceptions and violations of individual fairness: e.g., the price seen by a customer can be significantly higher than what was seen by her predecessors, only to fall once again later. To address this concern, we propose demand learning under a monotonicity constraint on the sequence of prices, within the framework of stochastic convex optimization with bandit feedback. Our main contribution is the design of the first sublinear-regret algorithms for monotonic price experimentation for smooth and strongly concave revenue functions under noisy as well as noiseless bandit feedback. The monotonicity constraint presents a unique challenge: since any increase (or decrease) in the decision-levels is final, an algorithm needs to be cautious in its exploration to avoid over-shooting the optimum. At the same time, minimizing regret requires that progress be made towards the optimum at a sufficient pace. Balancing these two goals is particularly challenging under noisy feedback, where obtaining sufficiently accurate gradient estimates is expensive. Our key innovation is to utilize conservative gradient estimates to adaptively tailor the degree of caution to local gradient information, being aggressive far from the optimum and being increasingly cautious as the prices approach the optimum. Importantly, we show that our algorithms guarantee the same regret rates (up to logarithmic factors) as the best achievable rates of regret without the monotonicity requirement.

Multi-Threshold Attention U-Net based Model for Multimodal Brain Tumor Segmentation in MRI scans

Gliomas are one of the most frequent brain tumors and are classified into high grade and low grade gliomas. The segmentation of various regions such as tumor core, enhancing tumor etc. plays an important role in determining severity and prognosis. Here, we have developed a multi-threshold model based on attention U-Net for identification of various regions of the tumor in magnetic resonance imaging (MRI). We propose a multi-path segmentation and built three separate models for the different regions of interest. The proposed model achieved mean Dice Coefficient of 0.59, 0.72, and 0.61 for enhancing tumor, whole tumor and tumor core respectively on the training dataset. The same model gave mean Dice Coefficient of 0.57, 0.73, and 0.61 on the validation dataset and 0.59, 0.72, and 0.57 on the test dataset.

Walking in the Shadow: A New Perspective on Descent Directions for Constrained Minimization

Descent directions such as movement towards Frank-Wolfe vertices, away steps, in-face away steps and pairwise directions have been an important design consideration in conditional gradient descent (CGD) variants. In this work, we attempt to demystify the impact of movement in these directions towards attaining constrained minimizers. The best local direction of descent is the directional derivative of the projection of the gradient, which we refer to as the $\textit{shadow}$ of the gradient. We show that the continuous-time dynamics of moving in the shadow are equivalent to those of PGD however non-trivial to discretize. By projecting gradients in PGD, one not only ensures feasibility but also is able to "wrap" around the convex region. We show that Frank-Wolfe (FW) vertices in fact recover the maximal wrap one can obtain by projecting gradients, thus providing a new perspective to these steps. We also claim that the shadow steps give the best direction of descent emanating from the convex hull of all possible away-vertices. Opening up the PGD movements in terms of shadow steps gives linear convergence, dependent on the number of faces. We combine these insights into a novel $S\small{HADOW}$-$CG$ method that uses FW steps (i.e., wrap around the polytope) and shadow steps (i.e., optimal local descent direction), while enjoying linear convergence. Our analysis develops properties of directional derivatives of projections (which may be of independent interest), while providing a unifying view of various descent directions in the CGD literature.

Group-Fair Online Allocation in Continuous Time

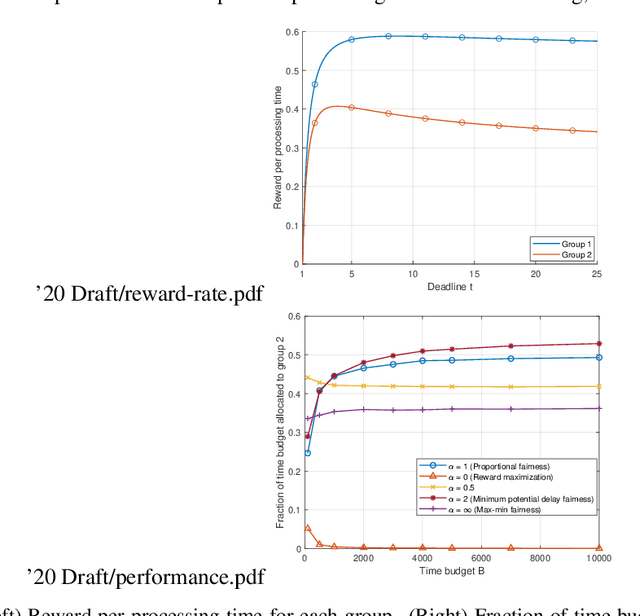
The theory of discrete-time online learning has been successfully applied in many problems that involve sequential decision-making under uncertainty. However, in many applications including contractual hiring in online freelancing platforms and server allocation in cloud computing systems, the outcome of each action is observed only after a random and action-dependent time. Furthermore, as a consequence of certain ethical and economic concerns, the controller may impose deadlines on the completion of each task, and require fairness across different groups in the allocation of total time budget $B$. In order to address these applications, we consider continuous-time online learning problem with fairness considerations, and present a novel framework based on continuous-time utility maximization. We show that this formulation recovers reward-maximizing, max-min fair and proportionally fair allocation rules across different groups as special cases. We characterize the optimal offline policy, which allocates the total time between different actions in an optimally fair way (as defined by the utility function), and impose deadlines to maximize time-efficiency. In the absence of any statistical knowledge, we propose a novel online learning algorithm based on dual ascent optimization for time averages, and prove that it achieves $\tilde{O}(B^{-1/2})$ regret bound.

Impact of Bias on School Admissions and Targeted Interventions

There is an inherent problem in the way students are evaluated - be it standardized testing, interviews or essays. These evaluation criteria cannot be adjusted to account for the impact of implicit bias, socio-economic status or even opportunities available to the students. Motivated by this, we present, to the best of our knowledge, the first mathematical analysis of the impact of deficiencies in evaluation mechanisms on the rank of schools that students get matched to. In particular, we analyze a double continuous model of schools and students, where all the students have a unanimous ranking for all the schools, and schools observe the potential of students to accept the best students from the available applicant pool. To account for bias in evaluations, we consider the group model of bias (Kleinberg and Raghavan 2018) where the schools can only observe a discounted potential for a subset of the candidates, instead of their actual potential. We show that under a natural matching mechanism, the ranking of the matched schools of both unbiased group and biased group of students are affected, with some of the latter being heavily penalized even for relatively small bias. Further, we find that schools have little incentive to change their evaluation mechanism, if their goal is the maximize the total potential of accepted students. Armed with this basic model and inferences, we show that the students who are most in need of additional resources to achieve their true potential are average-performing students, as opposed to high performers, thus questioning existing scholarship/aide mechanisms focusing on top performers. We further show, using computational experiments, that the qualitative take-aways from our model remain the same even if some of the assumptions are relaxed and we move, e.g., from a continuous to a discrete model and allow the bias factor to vary for each student.