Atilla Eryilmaz
Finite-Time Analysis of Gradient Descent for Shallow Transformers
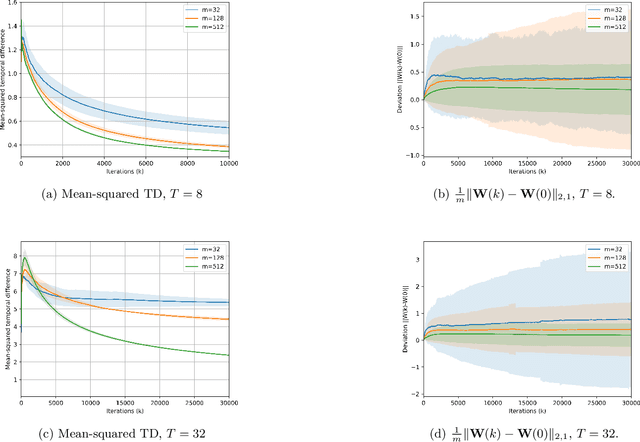
Jan 23, 2026Abstract:Understanding why Transformers perform so well remains challenging due to their non-convex optimization landscape. In this work, we analyze a shallow Transformer with $m$ independent heads trained by projected gradient descent in the kernel regime. Our analysis reveals two main findings: (i) the width required for nonasymptotic guarantees scales only logarithmically with the sample size $n$, and (ii) the optimization error is independent of the sequence length $T$. This contrasts sharply with recurrent architectures, where the optimization error can grow exponentially with $T$. The trade-off is memory: to keep the full context, the Transformer's memory requirement grows with the sequence length. We validate our theoretical results numerically in a teacher-student setting and confirm the predicted scaling laws for Transformers.
BeST -- A Novel Source Selection Metric for Transfer Learning
Jan 19, 2025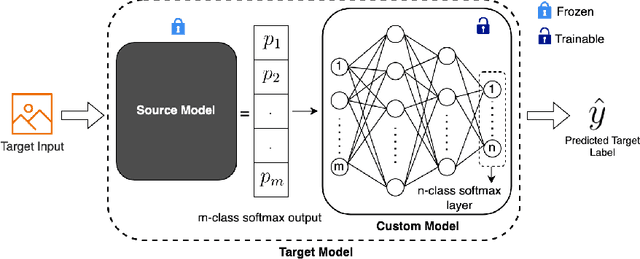

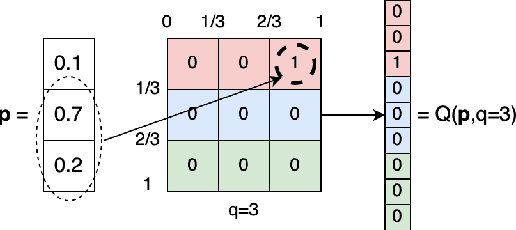

Abstract:One of the most fundamental, and yet relatively less explored, goals in transfer learning is the efficient means of selecting top candidates from a large number of previously trained models (optimized for various "source" tasks) that would perform the best for a new "target" task with a limited amount of data. In this paper, we undertake this goal by developing a novel task-similarity metric (BeST) and an associated method that consistently performs well in identifying the most transferrable source(s) for a given task. In particular, our design employs an innovative quantization-level optimization procedure in the context of classification tasks that yields a measure of similarity between a source model and the given target data. The procedure uses a concept similar to early stopping (usually implemented to train deep neural networks (DNNs) to ensure generalization) to derive a function that approximates the transfer learning mapping without training. The advantage of our metric is that it can be quickly computed to identify the top candidate(s) for a given target task before a computationally intensive transfer operation (typically using DNNs) can be implemented between the selected source and the target task. As such, our metric can provide significant computational savings for transfer learning from a selection of a large number of possible source models. Through extensive experimental evaluations, we establish that our metric performs well over different datasets and varying numbers of data samples.
Non-Federated Multi-Task Split Learning for Heterogeneous Sources
May 31, 2024Abstract:With the development of edge networks and mobile computing, the need to serve heterogeneous data sources at the network edge requires the design of new distributed machine learning mechanisms. As a prevalent approach, Federated Learning (FL) employs parameter-sharing and gradient-averaging between clients and a server. Despite its many favorable qualities, such as convergence and data-privacy guarantees, it is well-known that classic FL fails to address the challenge of data heterogeneity and computation heterogeneity across clients. Most existing works that aim to accommodate such sources of heterogeneity stay within the FL operation paradigm, with modifications to overcome the negative effect of heterogeneous data. In this work, as an alternative paradigm, we propose a Multi-Task Split Learning (MTSL) framework, which combines the advantages of Split Learning (SL) with the flexibility of distributed network architectures. In contrast to the FL counterpart, in this paradigm, heterogeneity is not an obstacle to overcome, but a useful property to take advantage of. As such, this work aims to introduce a new architecture and methodology to perform multi-task learning for heterogeneous data sources efficiently, with the hope of encouraging the community to further explore the potential advantages we reveal. To support this promise, we first show through theoretical analysis that MTSL can achieve fast convergence by tuning the learning rate of the server and clients. Then, we compare the performance of MTSL with existing multi-task FL methods numerically on several image classification datasets to show that MTSL has advantages over FL in training speed, communication cost, and robustness to heterogeneous data.
Recurrent Natural Policy Gradient for POMDPs
May 28, 2024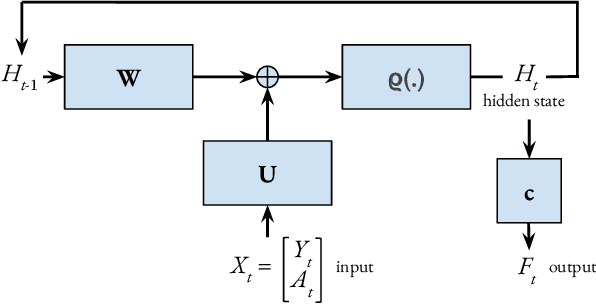
Abstract:In this paper, we study a natural policy gradient method based on recurrent neural networks (RNNs) for partially-observable Markov decision processes, whereby RNNs are used for policy parameterization and policy evaluation to address curse of dimensionality in non-Markovian reinforcement learning. We present finite-time and finite-width analyses for both the critic (recurrent temporal difference learning), and correspondingly-operated recurrent natural policy gradient method in the near-initialization regime. Our analysis demonstrates the efficiency of RNNs for problems with short-term memory with explicit bounds on the required network widths and sample complexity, and points out the challenges in the case of long-term dependencies.
Convergence of Gradient Descent for Recurrent Neural Networks: A Nonasymptotic Analysis
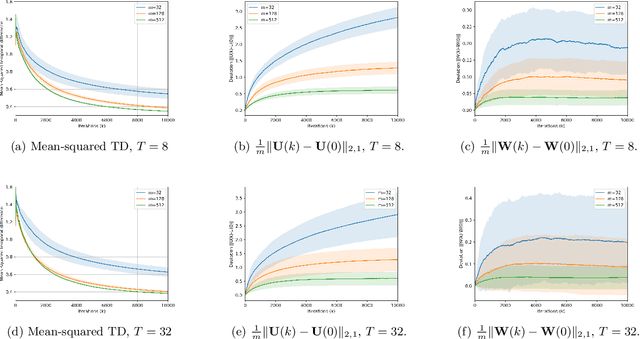
Feb 19, 2024Abstract:We analyze recurrent neural networks trained with gradient descent in the supervised learning setting for dynamical systems, and prove that gradient descent can achieve optimality \emph{without} massive overparameterization. Our in-depth nonasymptotic analysis (i) provides sharp bounds on the network size $m$ and iteration complexity $\tau$ in terms of the sequence length $T$, sample size $n$ and ambient dimension $d$, and (ii) identifies the significant impact of long-term dependencies in the dynamical system on the convergence and network width bounds characterized by a cutoff point that depends on the Lipschitz continuity of the activation function. Remarkably, this analysis reveals that an appropriately-initialized recurrent neural network trained with $n$ samples can achieve optimality with a network size $m$ that scales only logarithmically with $n$. This sharply contrasts with the prior works that require high-order polynomial dependency of $m$ on $n$ to establish strong regularity conditions. Our results are based on an explicit characterization of the class of dynamical systems that can be approximated and learned by recurrent neural networks via norm-constrained transportation mappings, and establishing local smoothness properties of the hidden state with respect to the learnable parameters.
Provably Robust Temporal Difference Learning for Heavy-Tailed Rewards
Jun 20, 2023Abstract:In a broad class of reinforcement learning applications, stochastic rewards have heavy-tailed distributions, which lead to infinite second-order moments for stochastic (semi)gradients in policy evaluation and direct policy optimization. In such instances, the existing RL methods may fail miserably due to frequent statistical outliers. In this work, we establish that temporal difference (TD) learning with a dynamic gradient clipping mechanism, and correspondingly operated natural actor-critic (NAC), can be provably robustified against heavy-tailed reward distributions. It is shown in the framework of linear function approximation that a favorable tradeoff between bias and variability of the stochastic gradients can be achieved with this dynamic gradient clipping mechanism. In particular, we prove that robust versions of TD learning achieve sample complexities of order $\mathcal{O}(\varepsilon^{-\frac{1}{p}})$ and $\mathcal{O}(\varepsilon^{-1-\frac{1}{p}})$ with and without the full-rank assumption on the feature matrix, respectively, under heavy-tailed rewards with finite moments of order $(1+p)$ for some $p\in(0,1]$, both in expectation and with high probability. We show that a robust variant of NAC based on Robust TD learning achieves $\tilde{\mathcal{O}}(\varepsilon^{-4-\frac{2}{p}})$ sample complexity. We corroborate our theoretical results with numerical experiments.
A Lyapunov-Based Methodology for Constrained Optimization with Bandit Feedback
Jun 09, 2021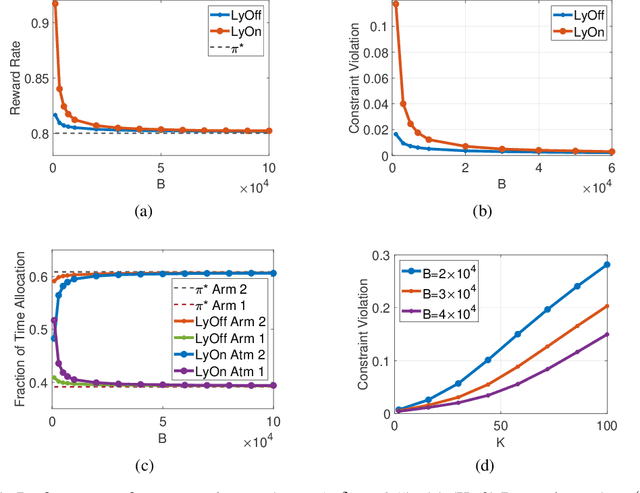
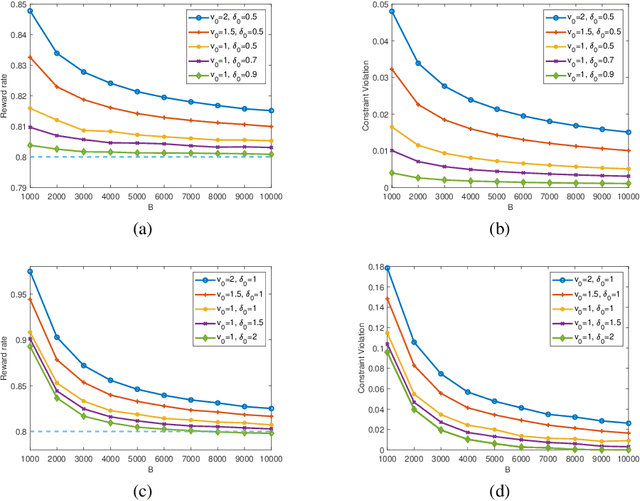
Abstract:In a wide variety of applications including online advertising, contractual hiring, and wireless scheduling, the controller is constrained by a stringent budget constraint on the available resources, which are consumed in a random amount by each action, and a stochastic feasibility constraint that may impose important operational limitations on decision-making. In this work, we consider a general model to address such problems, where each action returns a random reward, cost, and penalty from an unknown joint distribution, and the decision-maker aims to maximize the total reward under a budget constraint $B$ on the total cost and a stochastic constraint on the time-average penalty. We propose a novel low-complexity algorithm based on Lyapunov optimization methodology, named ${\tt LyOn}$, and prove that it achieves $O(\sqrt{B\log B})$ regret and $O(\log B/B)$ constraint-violation. The low computational cost and sharp performance bounds of ${\tt LyOn}$ suggest that Lyapunov-based algorithm design methodology can be effective in solving constrained bandit optimization problems.
Continuous-Time Multi-Armed Bandits with Controlled Restarts
Jun 30, 2020
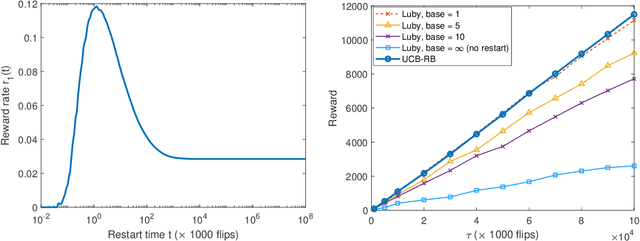
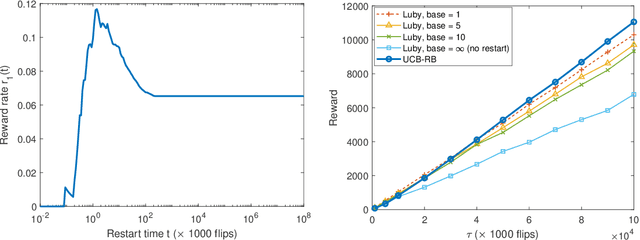
Abstract:Time-constrained decision processes have been ubiquitous in many fundamental applications in physics, biology and computer science. Recently, restart strategies have gained significant attention for boosting the efficiency of time-constrained processes by expediting the completion times. In this work, we investigate the bandit problem with controlled restarts for time-constrained decision processes, and develop provably good learning algorithms. In particular, we consider a bandit setting where each decision takes a random completion time, and yields a random and correlated reward at the end, with unknown values at the time of decision. The goal of the decision-maker is to maximize the expected total reward subject to a time constraint $\tau$. As an additional control, we allow the decision-maker to interrupt an ongoing task and forgo its reward for a potentially more rewarding alternative. For this problem, we develop efficient online learning algorithms with $O(\log(\tau))$ and $O(\sqrt{\tau\log(\tau)})$ regret in a finite and continuous action space of restart strategies, respectively. We demonstrate an applicability of our algorithm by using it to boost the performance of SAT solvers.
Group-Fair Online Allocation in Continuous Time
Jun 11, 2020
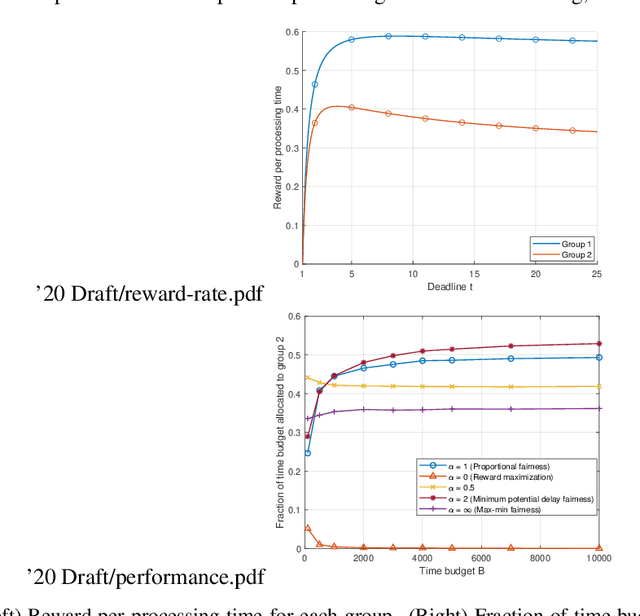
Abstract:The theory of discrete-time online learning has been successfully applied in many problems that involve sequential decision-making under uncertainty. However, in many applications including contractual hiring in online freelancing platforms and server allocation in cloud computing systems, the outcome of each action is observed only after a random and action-dependent time. Furthermore, as a consequence of certain ethical and economic concerns, the controller may impose deadlines on the completion of each task, and require fairness across different groups in the allocation of total time budget $B$. In order to address these applications, we consider continuous-time online learning problem with fairness considerations, and present a novel framework based on continuous-time utility maximization. We show that this formulation recovers reward-maximizing, max-min fair and proportionally fair allocation rules across different groups as special cases. We characterize the optimal offline policy, which allocates the total time between different actions in an optimally fair way (as defined by the utility function), and impose deadlines to maximize time-efficiency. In the absence of any statistical knowledge, we propose a novel online learning algorithm based on dual ascent optimization for time averages, and prove that it achieves $\tilde{O}(B^{-1/2})$ regret bound.
Budget-Constrained Bandits over General Cost and Reward Distributions
Feb 29, 2020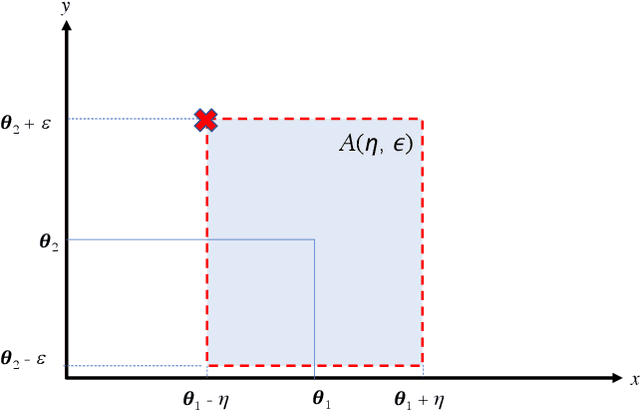
Abstract:We consider a budget-constrained bandit problem where each arm pull incurs a random cost, and yields a random reward in return. The objective is to maximize the total expected reward under a budget constraint on the total cost. The model is general in the sense that it allows correlated and potentially heavy-tailed cost-reward pairs that can take on negative values as required by many applications. We show that if moments of order $(2+\gamma)$ for some $\gamma > 0$ exist for all cost-reward pairs, $O(\log B)$ regret is achievable for a budget $B>0$. In order to achieve tight regret bounds, we propose algorithms that exploit the correlation between the cost and reward of each arm by extracting the common information via linear minimum mean-square error estimation. We prove a regret lower bound for this problem, and show that the proposed algorithms achieve tight problem-dependent regret bounds, which are optimal up to a universal constant factor in the case of jointly Gaussian cost and reward pairs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge