A Lyapunov-Based Methodology for Constrained Optimization with Bandit Feedback
Paper and Code
Jun 09, 2021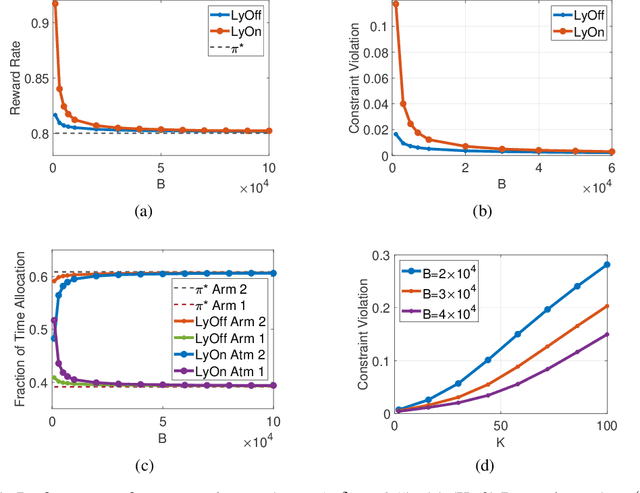
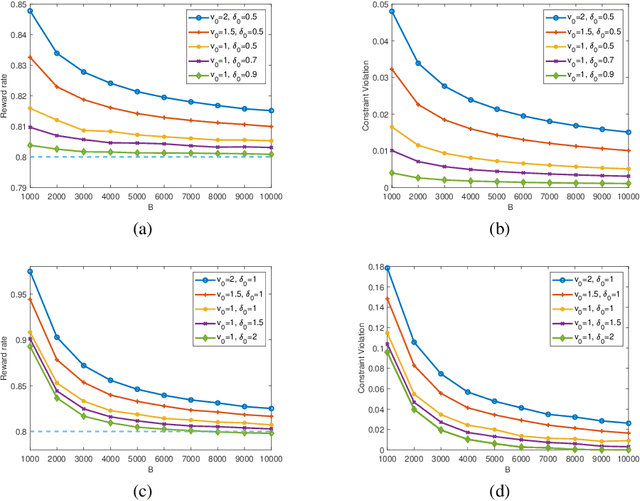
In a wide variety of applications including online advertising, contractual hiring, and wireless scheduling, the controller is constrained by a stringent budget constraint on the available resources, which are consumed in a random amount by each action, and a stochastic feasibility constraint that may impose important operational limitations on decision-making. In this work, we consider a general model to address such problems, where each action returns a random reward, cost, and penalty from an unknown joint distribution, and the decision-maker aims to maximize the total reward under a budget constraint $B$ on the total cost and a stochastic constraint on the time-average penalty. We propose a novel low-complexity algorithm based on Lyapunov optimization methodology, named ${\tt LyOn}$, and prove that it achieves $O(\sqrt{B\log B})$ regret and $O(\log B/B)$ constraint-violation. The low computational cost and sharp performance bounds of ${\tt LyOn}$ suggest that Lyapunov-based algorithm design methodology can be effective in solving constrained bandit optimization problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge