Optimal Learning for Dynamic Coding in Deadline-Constrained Multi-Channel Networks
Paper and Code
Nov 27, 2018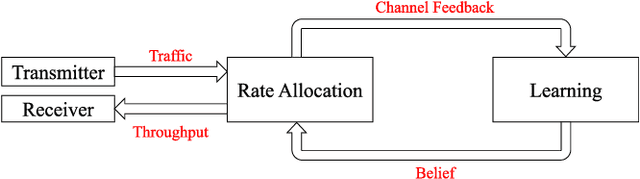
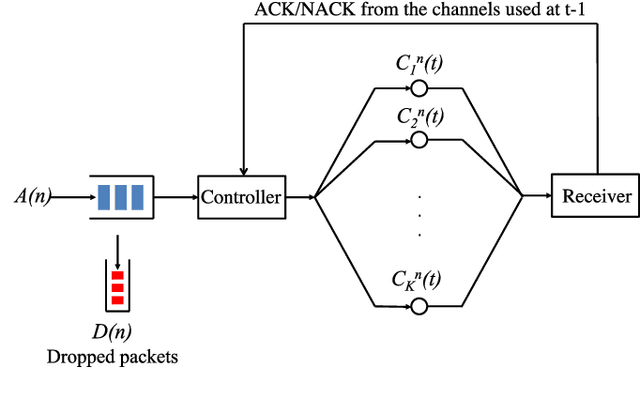
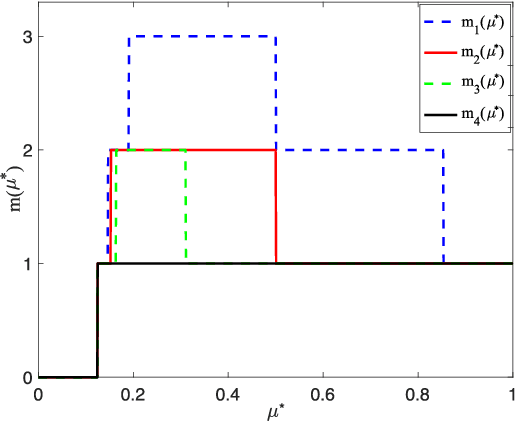
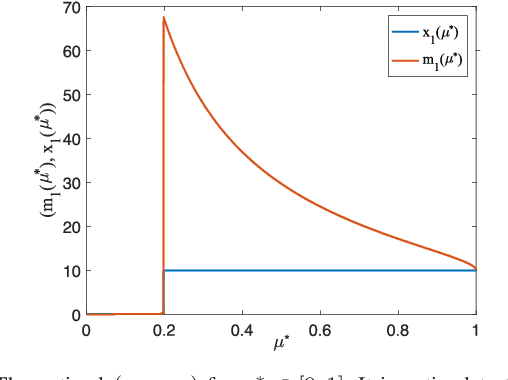
We study the problem of serving randomly arriving and delay-sensitive traffic over a multi-channel communication system with time-varying channel states and unknown statistics. This problem deviates from the classical exploration-exploitation setting in that the design and analysis must accommodate the dynamics of packet availability and urgency as well as the cost of each channel use at the time of decision. To that end, we have developed and investigated an index-based policy UCB-Deadline, which performs dynamic channel allocation decisions that incorporate these traffic requirements and costs. Under symmetric channel conditions, we have proved that the UCB-Deadline policy can achieve bounded regret in the likely case where the cost of using a channel is not too high to prevent all transmissions, and logarithmic regret otherwise. In this case, we show that UCB-Deadline is order-optimal. We also perform numerical investigations to validate the theoretical findings, and also compare the performance of the UCB-Deadline to another learning algorithm that we propose based on Thompson Sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge