Bistra Dilkina
ID-PaS : Identity-Aware Predict-and-Search for General Mixed-Integer Linear Programs
Dec 11, 2025Abstract:Mixed-Integer Linear Programs (MIPs) are powerful and flexible tools for modeling a wide range of real-world combinatorial optimization problems. Predict-and-Search methods operate by using a predictive model to estimate promising variable assignments and then guiding a search procedure toward high-quality solutions. Recent research has demonstrated that incorporating machine learning (ML) into the Predict-and-Search framework significantly enhances its performance. Still, it is restricted to binary problems and overlooks the presence of fixed variables that commonly arise in practical settings. This work extends the Predict-and-Search (PaS) framework to parametric MIPs and introduces ID-PaS, an identity-aware learning framework that enables the ML model to handle heterogeneous variables more effectively. Experiments on several real-world large-scale problems demonstrate that ID-PaS consistently achieves superior performance compared to the state-of-the-art solver Gurobi and PaS.
LSPO: Length-aware Dynamic Sampling for Policy Optimization in LLM Reasoning
Oct 01, 2025Abstract:Since the release of Deepseek-R1, reinforcement learning with verifiable rewards (RLVR) has become a central approach for training large language models (LLMs) on reasoning tasks. Recent work has largely focused on modifying loss functions to make RLVR more efficient and effective. In this paper, motivated by studies of overthinking in LLMs, we propose Length-aware Sampling for Policy Optimization (LSPO), a novel meta-RLVR algorithm that dynamically selects training data at each step based on the average response length. We evaluate LSPO across multiple base models and datasets, demonstrating that it consistently improves learning effectiveness. In addition, we conduct a detailed ablation study to examine alternative ways of incorporating length signals into dynamic sampling, offering further insights and highlighting promising directions for future research.
Global Constraint LLM Agents for Text-to-Model Translation
Sep 10, 2025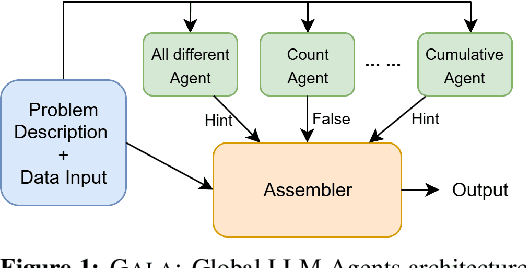

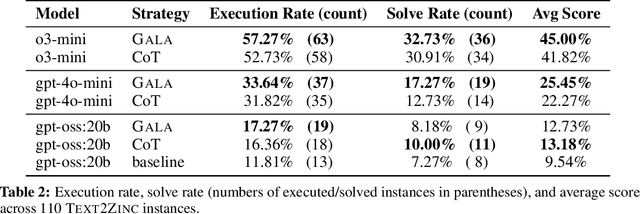
Abstract:Natural language descriptions of optimization or satisfaction problems are challenging to translate into correct MiniZinc models, as this process demands both logical reasoning and constraint programming expertise. We introduce a framework that addresses this challenge with an agentic approach: multiple specialized large language model (LLM) agents decompose the modeling task by global constraint type. Each agent is dedicated to detecting and generating code for a specific class of global constraint, while a final assembler agent integrates these constraint snippets into a complete MiniZinc model. By dividing the problem into smaller, well-defined sub-tasks, each LLM handles a simpler reasoning challenge, potentially reducing overall complexity. We conduct initial experiments with several LLMs and show better performance against baselines such as one-shot prompting and chain-of-thought prompting. Finally, we outline a comprehensive roadmap for future work, highlighting potential enhancements and directions for improvement.
Iterative Deepening Sampling for Large Language Models
Feb 08, 2025
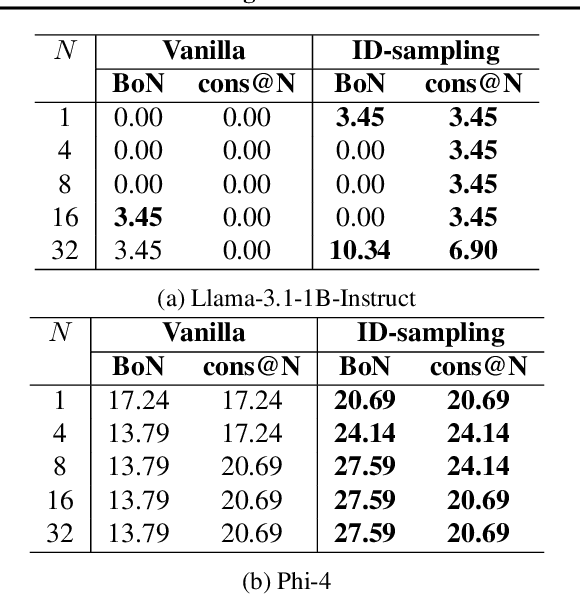
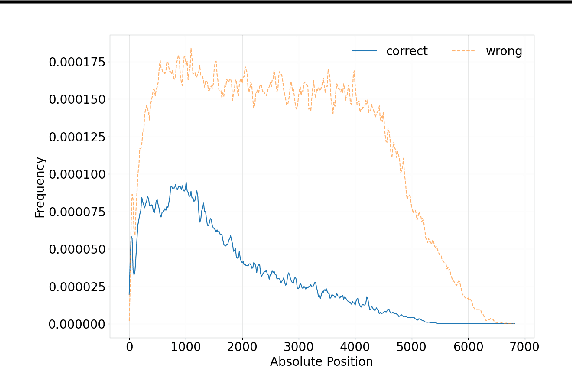
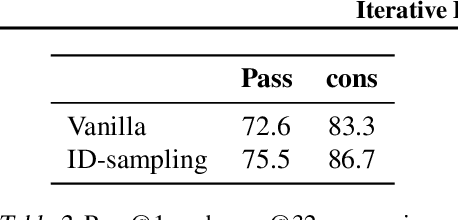
Abstract:The recent release of OpenAI's o1 models and other similar frameworks showcasing test-time scaling laws has demonstrated their exceptional capability to tackle complex reasoning tasks. Inspired by this, subsequent research has revealed that such test-time scaling laws hinge on the model's ability to search both within a single response (intra-response) and across multiple responses (inter-response) during training. Crucially, beyond selecting a single optimal response, the model must also develop robust self-correction capabilities within its own outputs. However, training models to achieve effective self-evaluation and self-correction remains a significant challenge, heavily dependent on the quality of self-reflection data. In this paper, we address this challenge by focusing on enhancing the quality of self-reflection data generation for complex problem-solving, which can subsequently improve the training of next-generation large language models (LLMs). Specifically, we explore how manually triggering a model's self-correction mechanisms can improve performance on challenging reasoning tasks. To this end, we propose a novel iterative deepening sampling algorithm framework designed to enhance self-correction and generate higher-quality samples. Through extensive experiments on Math500 and AIME benchmarks, we demonstrate that our method achieves a higher success rate on difficult tasks and provide detailed ablation studies to analyze its effectiveness across diverse settings.
Balans: Multi-Armed Bandits-based Adaptive Large Neighborhood Search for Mixed-Integer Programming Problem
Dec 18, 2024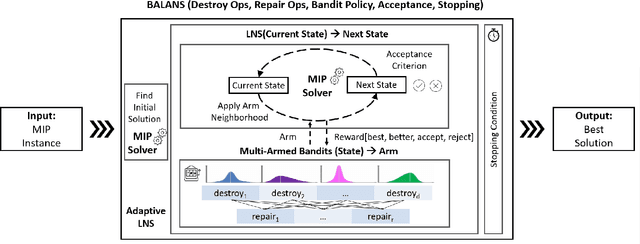
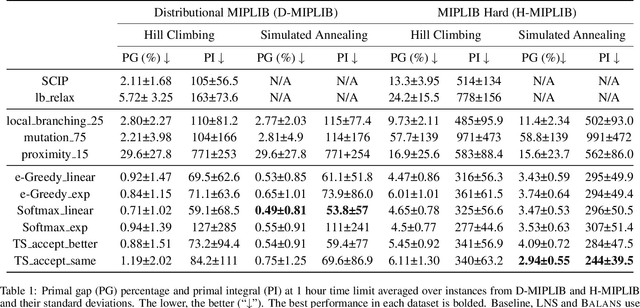
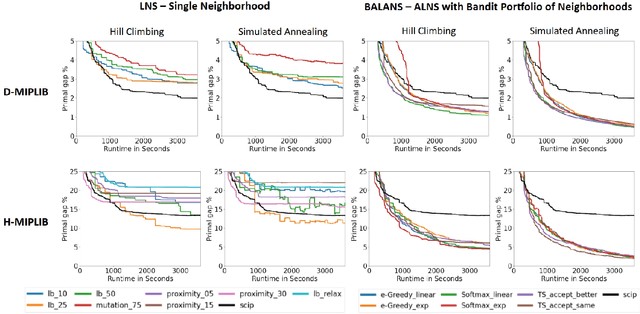

Abstract:Mixed-Integer Programming (MIP) is a powerful paradigm for modeling and solving various important combinatorial optimization problems. Recently, learning-based approaches have shown potential to speed up MIP solving via offline training that then guides important design decisions during search. However, a significant drawback of these methods is their heavy reliance on offline training, which requires collecting training datasets and computationally costly training epochs yet offering only limited generalization to unseen (larger) instances. In this paper, we propose Balans, an adaptive meta-solver for MIPs with online learning capability that does not require any supervision or apriori training. At its core, Balans is based on adaptive large-neighborhood search, operating on top of a MIP solver by successive applications of destroy and repair neighborhood operators. During the search, the selection among different neighborhood definitions is guided on the fly for the instance at hand via multi-armed bandit algorithms. Our extensive experiments on hard optimization instances show that Balans offers significant performance gains over the default MIP solver, is better than committing to any single best neighborhood, and improves over the state-of-the-art large-neighborhood search for MIPs. Finally, we release Balans as a highly configurable, MIP solver agnostic, open-source software.
Multi-task Representation Learning for Mixed Integer Linear Programming
Dec 18, 2024



Abstract:Mixed Integer Linear Programs (MILPs) are highly flexible and powerful tools for modeling and solving complex real-world combinatorial optimization problems. Recently, machine learning (ML)-guided approaches have demonstrated significant potential in improving MILP-solving efficiency. However, these methods typically rely on separate offline data collection and training processes, which limits their scalability and adaptability. This paper introduces the first multi-task learning framework for ML-guided MILP solving. The proposed framework provides MILP embeddings helpful in guiding MILP solving across solvers (e.g., Gurobi and SCIP) and across tasks (e.g., Branching and Solver configuration). Through extensive experiments on three widely used MILP benchmarks, we demonstrate that our multi-task learning model performs similarly to specialized models within the same distribution. Moreover, it significantly outperforms them in generalization across problem sizes and tasks.
RePrompt: Planning by Automatic Prompt Engineering for Large Language Models Agents
Jun 17, 2024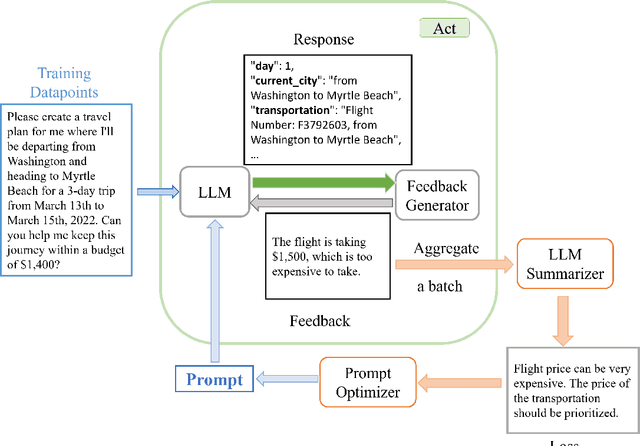

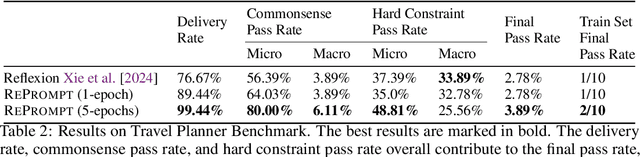

Abstract:In this past year, large language models (LLMs) have had remarkable success in domains outside the traditional natural language processing, and people are starting to explore the usage of LLMs in more general and close to application domains like code generation, travel planning, and robot controls. Connecting these LLMs with great capacity and external tools, people are building the so-called LLM agents, which are supposed to help people do all kinds of work in everyday life. In all these domains, the prompt to the LLMs has been shown to make a big difference in what the LLM would generate and thus affect the performance of the LLM agents. Therefore, automatic prompt engineering has become an important question for many researchers and users of LLMs. In this paper, we propose a novel method, \textsc{RePrompt}, which does "gradient descent" to optimize the step-by-step instructions in the prompt of the LLM agents based on the chat history obtained from interactions with LLM agents. By optimizing the prompt, the LLM will learn how to plan in specific domains. We have used experiments in PDDL generation and travel planning to show that our method could generally improve the performance for different reasoning tasks when using the updated prompt as the initial prompt.
Distributional MIPLIB: a Multi-Domain Library for Advancing ML-Guided MILP Methods
Jun 11, 2024Abstract:Mixed Integer Linear Programming (MILP) is a fundamental tool for modeling combinatorial optimization problems. Recently, a growing body of research has used machine learning to accelerate MILP solving. Despite the increasing popularity of this approach, there is a lack of a common repository that provides distributions of similar MILP instances across different domains, at different hardness levels, with standardized test sets. In this paper, we introduce Distributional MIPLIB, a multi-domain library of problem distributions for advancing ML-guided MILP methods. We curate MILP distributions from existing work in this area as well as real-world problems that have not been used, and classify them into different hardness levels. It will facilitate research in this area by enabling comprehensive evaluation on diverse and realistic domains. We empirically illustrate the benefits of using Distributional MIPLIB as a research vehicle in two ways. We evaluate the performance of ML-guided variable branching on previously unused distributions to identify potential areas for improvement. Moreover, we propose to learn branching policies from a mix of distributions, demonstrating that mixed distributions achieve better performance compared to homogeneous distributions when there is limited data and generalize well to larger instances.
MARL-LNS: Cooperative Multi-agent Reinforcement Learning via Large Neighborhoods Search
Apr 03, 2024



Abstract:Cooperative multi-agent reinforcement learning (MARL) has been an increasingly important research topic in the last half-decade because of its great potential for real-world applications. Because of the curse of dimensionality, the popular "centralized training decentralized execution" framework requires a long time in training, yet still cannot converge efficiently. In this paper, we propose a general training framework, MARL-LNS, to algorithmically address these issues by training on alternating subsets of agents using existing deep MARL algorithms as low-level trainers, while not involving any additional parameters to be trained. Based on this framework, we provide three algorithm variants based on the framework: random large neighborhood search (RLNS), batch large neighborhood search (BLNS), and adaptive large neighborhood search (ALNS), which alternate the subsets of agents differently. We test our algorithms on both the StarCraft Multi-Agent Challenge and Google Research Football, showing that our algorithms can automatically reduce at least 10% of training time while reaching the same final skill level as the original algorithm.
Application-Driven Innovation in Machine Learning
Mar 26, 2024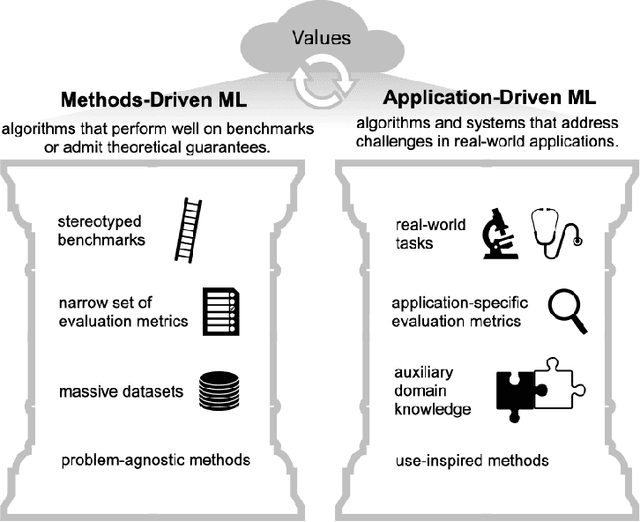
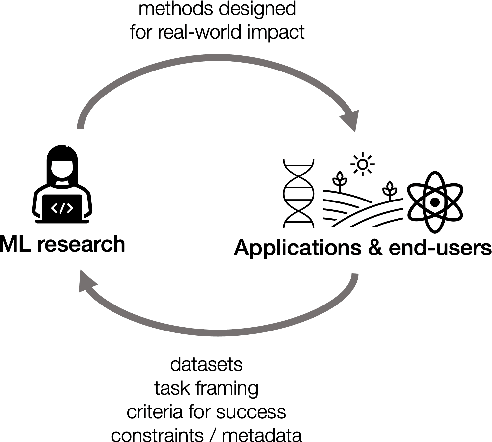
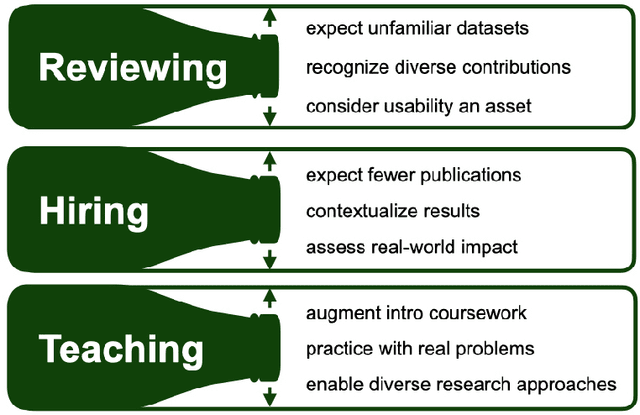
Abstract:As applications of machine learning proliferate, innovative algorithms inspired by specific real-world challenges have become increasingly important. Such work offers the potential for significant impact not merely in domains of application but also in machine learning itself. In this paper, we describe the paradigm of application-driven research in machine learning, contrasting it with the more standard paradigm of methods-driven research. We illustrate the benefits of application-driven machine learning and how this approach can productively synergize with methods-driven work. Despite these benefits, we find that reviewing, hiring, and teaching practices in machine learning often hold back application-driven innovation. We outline how these processes may be improved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge