BoolXLLM: LLM-Assisted Explainability for Boolean Models

Interpretable machine learning aims to provide transparent models whose decision-making processes can be readily understood by humans. Recent advances in rule-based approaches, such as expressive Boolean formulas (BoolXAI), offer faithful and compact representations of model behavior. However, for non-technical stakeholders, main challenges remain in practice: (i) selecting semantically meaningful features and (ii) translating formal logical rules into accessible explanations. In this work, we propose BoolXLLM , as a hybrid framework that integrates Large Language Models (LLMs) into the end-to-end pipeline of Boolean rule learning. We augment BoolXAI , an expressive Boolean rule-based classifier, with LLMs at three critical stages: (1) feature selection, where LLMs guide the identification of domain-relevant variables; (2) threshold recommendation, where LLMs propose semantically meaningful discretization strategies for numerical features; and (3) rule compression and interpretation, where Boolean rules are translated into natural language explanations at both global and local levels. This integration bridges formal, faithful explanations with human-understandable narratives. This allows build an explainable AI system that is both theoretically grounded and accessible to non-experts. Early empirical results demonstrate that LLM-assisted pipelines improve interpretability while maintaining competitive predictive performance. Our work highlights the promise of combining symbolic reasoning with language-based models for human-centered explainability.

Modeling Copilots for Text-to-Model Translation

There is growing interest in leveraging large language models (LLMs) for text-to-model translation and optimization tasks. This paper aims to advance this line of research by introducing \textsc{Text2Model} and \textsc{Text2Zinc}. \textsc{Text2Model} is a suite of copilots based on several LLM strategies with varying complexity, along with an online leaderboard. \textsc{Text2Zinc} is a cross-domain dataset for capturing optimization and satisfaction problems specified in natural language, along with an interactive editor with built-in AI assistant. While there is an emerging literature on using LLMs for translating combinatorial problems into formal models, our work is the first attempt to integrate \textit{both} satisfaction and optimization problems within a \textit{unified architecture} and \textit{dataset}. Moreover, our approach is \textit{solver-agnostic} unlike existing work that focuses on translation to a solver-specific model. To achieve this, we leverage \textsc{MiniZinc}'s solver-and-paradigm-agnostic modeling capabilities to formulate combinatorial problems. We conduct comprehensive experiments to compare execution and solution accuracy across several single- and multi-call strategies, including; zero-shot prompting, chain-of-thought reasoning, intermediate representations via knowledge-graphs, grammar-based syntax encoding, and agentic approaches that decompose the model into sequential sub-tasks. Our copilot strategies are competitive, and in parts improve, recent research in this domain. Our findings indicate that while LLMs are promising they are not yet a push-button technology for combinatorial modeling. We contribute \textsc{Text2Model} copilots and leaderboard, and \textsc{Text2Zinc} and interactive editor to open-source to support closing this performance gap.

Modeling Co-Pilots for Text-to-Model Translation

There is growing interest in leveraging large language models (LLMs) for text-to-model translation and optimization tasks. This paper aims to advance this line of research by introducing \textsc{Text2Model} and \textsc{Text2Zinc}. \textsc{Text2Model} is a suite of co-pilots based on several LLM strategies with varying complexity, along with an online leaderboard. \textsc{Text2Zinc} is a cross-domain dataset for capturing optimization and satisfaction problems specified in natural language, along with an interactive editor with built-in AI assistant. While there is an emerging literature on using LLMs for translating combinatorial problems into formal models, our work is the first attempt to integrate \textit{both} satisfaction and optimization problems within a \textit{unified architecture} and \textit{dataset}. Moreover, our approach is \textit{solver-agnostic} unlike existing work that focuses on translation to a solver-specific model. To achieve this, we leverage \textsc{MiniZinc}'s solver-and-paradigm-agnostic modeling capabilities to formulate combinatorial problems. We conduct comprehensive experiments to compare execution and solution accuracy across several single- and multi-call strategies, including; zero-shot prompting, chain-of-thought reasoning, intermediate representations via knowledge-graphs, grammar-based syntax encoding, and agentic approaches that decompose the model into sequential sub-tasks. Our co-pilot strategies are competitive, and in parts improve, recent research in this domain. Our findings indicate that while LLMs are promising they are not yet a push-button technology for combinatorial modeling. We contribute \textsc{Text2Model} co-pilots and leaderboard, and \textsc{Text2Zinc} and interactive editor to open-source to support closing this performance gap.

Global Constraint LLM Agents for Text-to-Model Translation

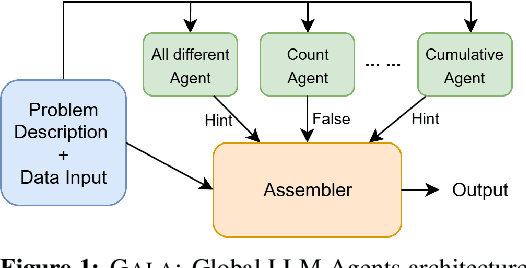
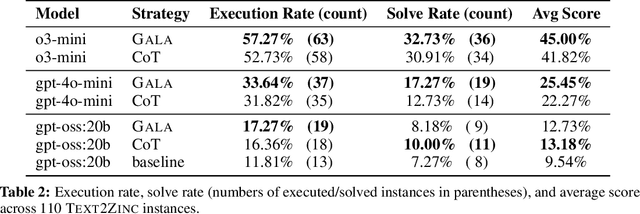
Natural language descriptions of optimization or satisfaction problems are challenging to translate into correct MiniZinc models, as this process demands both logical reasoning and constraint programming expertise. We introduce a framework that addresses this challenge with an agentic approach: multiple specialized large language model (LLM) agents decompose the modeling task by global constraint type. Each agent is dedicated to detecting and generating code for a specific class of global constraint, while a final assembler agent integrates these constraint snippets into a complete MiniZinc model. By dividing the problem into smaller, well-defined sub-tasks, each LLM handles a simpler reasoning challenge, potentially reducing overall complexity. We conduct initial experiments with several LLMs and show better performance against baselines such as one-shot prompting and chain-of-thought prompting. Finally, we outline a comprehensive roadmap for future work, highlighting potential enhancements and directions for improvement.

Balans: Multi-Armed Bandits-based Adaptive Large Neighborhood Search for Mixed-Integer Programming Problem

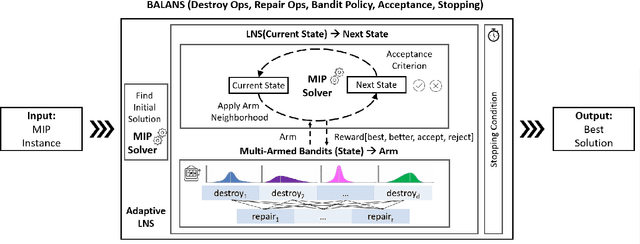
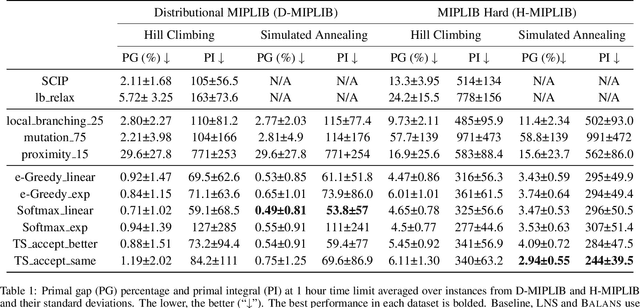
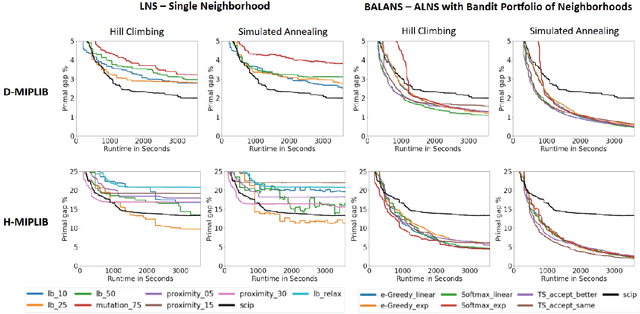
Mixed-Integer Programming (MIP) is a powerful paradigm for modeling and solving various important combinatorial optimization problems. Recently, learning-based approaches have shown potential to speed up MIP solving via offline training that then guides important design decisions during search. However, a significant drawback of these methods is their heavy reliance on offline training, which requires collecting training datasets and computationally costly training epochs yet offering only limited generalization to unseen (larger) instances. In this paper, we propose Balans, an adaptive meta-solver for MIPs with online learning capability that does not require any supervision or apriori training. At its core, Balans is based on adaptive large-neighborhood search, operating on top of a MIP solver by successive applications of destroy and repair neighborhood operators. During the search, the selection among different neighborhood definitions is guided on the fly for the instance at hand via multi-armed bandit algorithms. Our extensive experiments on hard optimization instances show that Balans offers significant performance gains over the default MIP solver, is better than committing to any single best neighborhood, and improves over the state-of-the-art large-neighborhood search for MIPs. Finally, we release Balans as a highly configurable, MIP solver agnostic, open-source software.

Dichotomic Pattern Mining with Applications to Intent Prediction from Semi-Structured Clickstream Datasets

We introduce a pattern mining framework that operates on semi-structured datasets and exploits the dichotomy between outcomes. Our approach takes advantage of constraint reasoning to find sequential patterns that occur frequently and exhibit desired properties. This allows the creation of novel pattern embeddings that are useful for knowledge extraction and predictive modeling. Finally, we present an application on customer intent prediction from digital clickstream data. Overall, we show that pattern embeddings play an integrator role between semi-structured data and machine learning models, improve the performance of the downstream task and retain interpretability.

Integrated Vehicle Routing and Monte Carlo Scheduling Approach for the Home Service Assignment, Routing, and Scheduling Problem

We formulate and solve the H-SARA Problem, a Vehicle Routing and Appointment Scheduling Problem motivated by home services management. We assume that travel times, service durations, and customer cancellations are stochastic. We use a two-stage process that first generates teams and routes using a VRP Solver with optional extensions and then uses an MC Scheduler that determines expected arrival times by teams at customers. We further introduce two different models of cancellation and their associated impacts on routing and scheduling. Finally, we introduce the Route Fracture Metaheuristic that iteratively improves an H-SARA solution by replacing the worst-performing teams. We present insights into the problem and a series of numerical experiments that illustrate properties of the optimal routing, scheduling, and the impact of the Route Fracture Metaheuristic for both models of cancellation.

Column Generation for Interaction Coverage in Combinatorial Software Testing

This paper proposes a novel column generation framework for combinatorial software testing. In particular, it combines Mathematical Programming and Constraint Programming in a hybrid decomposition to generate covering arrays. The approach allows generating parameterized test cases with coverage guarantees between parameter interactions of a given application. Compared to exhaustive testing, combinatorial test case generation reduces the number of tests to run significantly. Our column generation algorithm is generic and can accommodate mixed coverage arrays over heterogeneous alphabets. The algorithm is realized in practice as a cloud service and recognized as one of the five winners of the company-wide cloud application challenge at Oracle. The service is currently helping software developers from a range of different product teams in their testing efforts while exposing declarative constraint models and hybrid optimization techniques to a broader audience.

Transformation-based Feature Computation for Algorithm Portfolios

Instance-specific algorithm configuration and algorithm portfolios have been shown to offer significant improvements over single algorithm approaches in a variety of application domains. In the SAT and CSP domains algorithm portfolios have consistently dominated the main competitions in these fields for the past five years. For a portfolio approach to be effective there are two crucial conditions that must be met. First, there needs to be a collection of complementary solvers with which to make a portfolio. Second, there must be a collection of problem features that can accurately identify structural differences between instances. This paper focuses on the latter issue: feature representation, because, unlike SAT, not every problem has well-studied features. We employ the well-known SATzilla feature set, but compute alternative sets on different SAT encodings of CSPs. We show that regardless of what encoding is used to convert the instances, adequate structural information is maintained to differentiate between problem instances, and that this can be exploited to make an effective portfolio-based CSP solver.

DASH: Dynamic Approach for Switching Heuristics

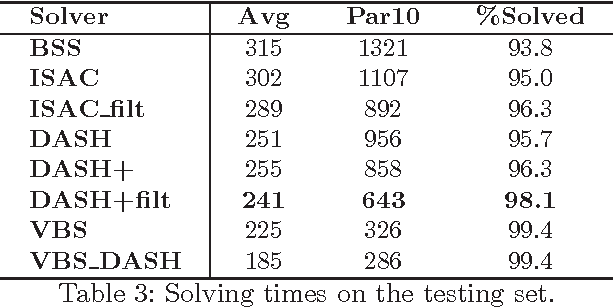
Complete tree search is a highly effective method for tackling MIP problems, and over the years, a plethora of branching heuristics have been introduced to further refine the technique for varying problems. Recently, portfolio algorithms have taken the process a step further, trying to predict the best heuristic for each instance at hand. However, the motivation behind algorithm selection can be taken further still, and used to dynamically choose the most appropriate algorithm for each encountered subproblem. In this paper we identify a feature space that captures both the evolution of the problem in the branching tree and the similarity among subproblems of instances from the same MIP models. We show how to exploit these features to decide the best time to switch the branching heuristic and then show how such a system can be trained efficiently. Experiments on a highly heterogeneous collection of MIP instances show significant gains over the pure algorithm selection approach that for a given instance uses only a single heuristic throughout the search.