DASH: Dynamic Approach for Switching Heuristics
Paper and Code
Jul 17, 2013


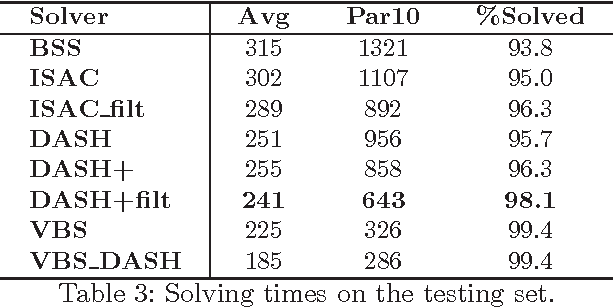
Complete tree search is a highly effective method for tackling MIP problems, and over the years, a plethora of branching heuristics have been introduced to further refine the technique for varying problems. Recently, portfolio algorithms have taken the process a step further, trying to predict the best heuristic for each instance at hand. However, the motivation behind algorithm selection can be taken further still, and used to dynamically choose the most appropriate algorithm for each encountered subproblem. In this paper we identify a feature space that captures both the evolution of the problem in the branching tree and the similarity among subproblems of instances from the same MIP models. We show how to exploit these features to decide the best time to switch the branching heuristic and then show how such a system can be trained efficiently. Experiments on a highly heterogeneous collection of MIP instances show significant gains over the pure algorithm selection approach that for a given instance uses only a single heuristic throughout the search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge