Yuri Malitsky
ASlib: A Benchmark Library for Algorithm Selection
Apr 06, 2016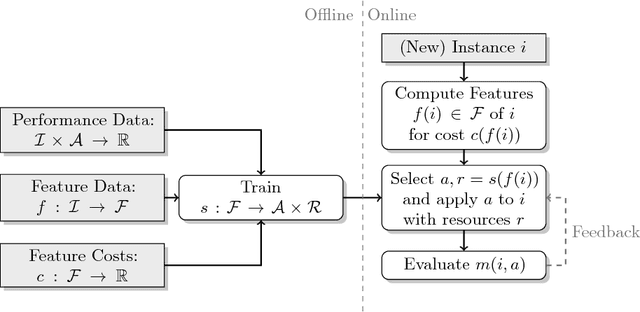
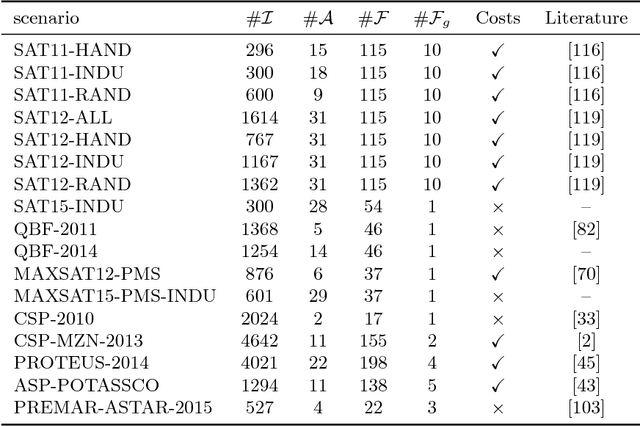
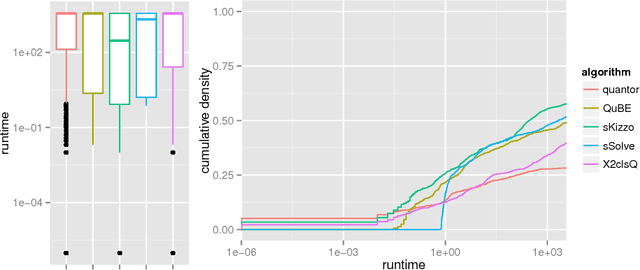
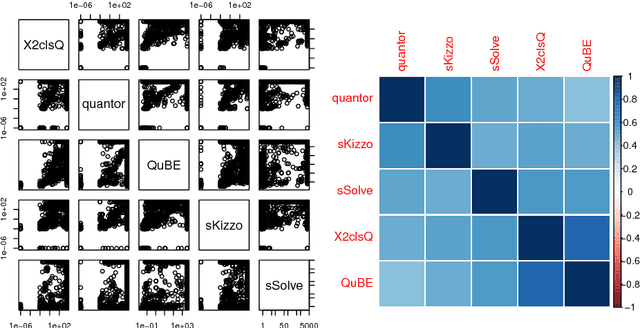
Abstract:The task of algorithm selection involves choosing an algorithm from a set of algorithms on a per-instance basis in order to exploit the varying performance of algorithms over a set of instances. The algorithm selection problem is attracting increasing attention from researchers and practitioners in AI. Years of fruitful applications in a number of domains have resulted in a large amount of data, but the community lacks a standard format or repository for this data. This situation makes it difficult to share and compare different approaches effectively, as is done in other, more established fields. It also unnecessarily hinders new researchers who want to work in this area. To address this problem, we introduce a standardized format for representing algorithm selection scenarios and a repository that contains a growing number of data sets from the literature. Our format has been designed to be able to express a wide variety of different scenarios. Demonstrating the breadth and power of our platform, we describe a set of example experiments that build and evaluate algorithm selection models through a common interface. The results display the potential of algorithm selection to achieve significant performance improvements across a broad range of problems and algorithms.
Proteus: A Hierarchical Portfolio of Solvers and Transformations
Feb 17, 2014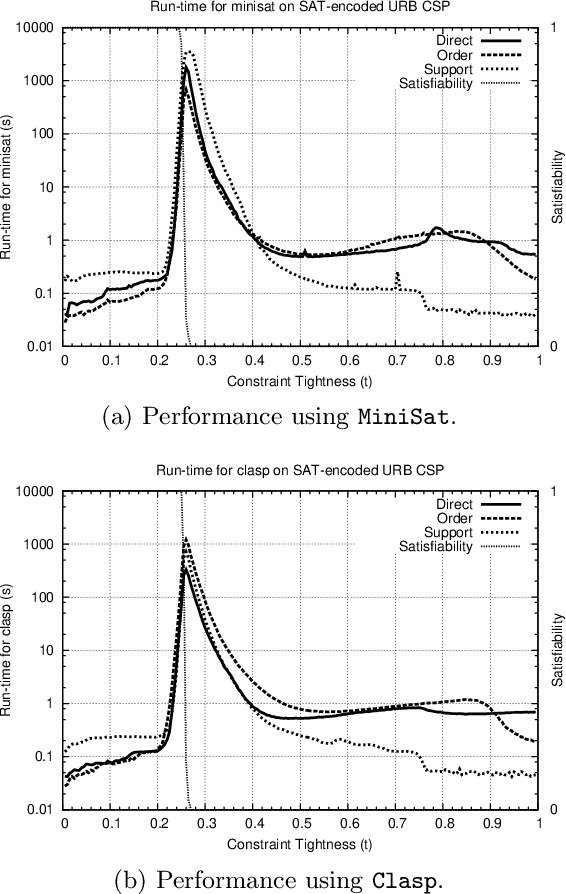
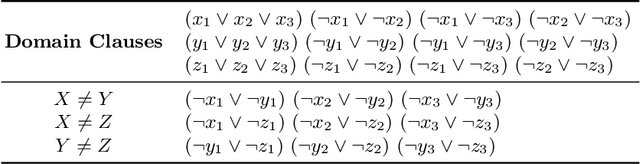
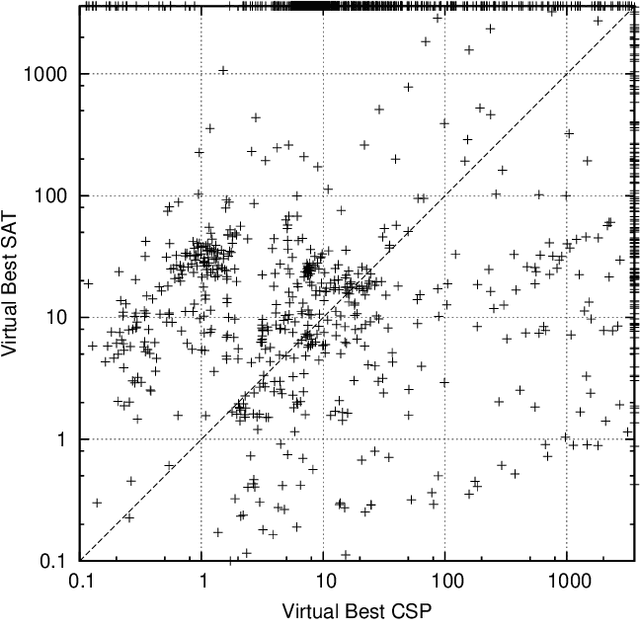
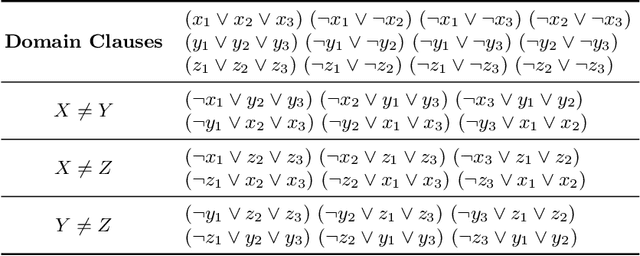
Abstract:In recent years, portfolio approaches to solving SAT problems and CSPs have become increasingly common. There are also a number of different encodings for representing CSPs as SAT instances. In this paper, we leverage advances in both SAT and CSP solving to present a novel hierarchical portfolio-based approach to CSP solving, which we call Proteus, that does not rely purely on CSP solvers. Instead, it may decide that it is best to encode a CSP problem instance into SAT, selecting an appropriate encoding and a corresponding SAT solver. Our experimental evaluation used an instance of Proteus that involved four CSP solvers, three SAT encodings, and six SAT solvers, evaluated on the most challenging problem instances from the CSP solver competitions, involving global and intensional constraints. We show that significant performance improvements can be achieved by Proteus obtained by exploiting alternative view-points and solvers for combinatorial problem-solving.
Transformation-based Feature Computation for Algorithm Portfolios
Jan 10, 2014
Abstract:Instance-specific algorithm configuration and algorithm portfolios have been shown to offer significant improvements over single algorithm approaches in a variety of application domains. In the SAT and CSP domains algorithm portfolios have consistently dominated the main competitions in these fields for the past five years. For a portfolio approach to be effective there are two crucial conditions that must be met. First, there needs to be a collection of complementary solvers with which to make a portfolio. Second, there must be a collection of problem features that can accurately identify structural differences between instances. This paper focuses on the latter issue: feature representation, because, unlike SAT, not every problem has well-studied features. We employ the well-known SATzilla feature set, but compute alternative sets on different SAT encodings of CSPs. We show that regardless of what encoding is used to convert the instances, adequate structural information is maintained to differentiate between problem instances, and that this can be exploited to make an effective portfolio-based CSP solver.
DASH: Dynamic Approach for Switching Heuristics
Jul 17, 2013


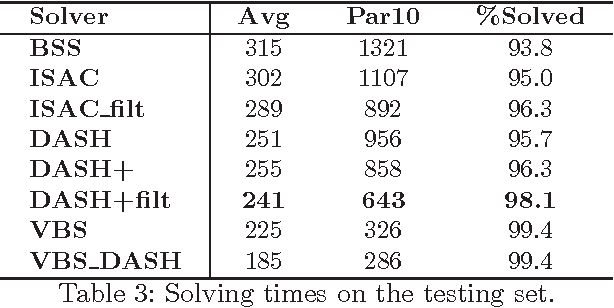
Abstract:Complete tree search is a highly effective method for tackling MIP problems, and over the years, a plethora of branching heuristics have been introduced to further refine the technique for varying problems. Recently, portfolio algorithms have taken the process a step further, trying to predict the best heuristic for each instance at hand. However, the motivation behind algorithm selection can be taken further still, and used to dynamically choose the most appropriate algorithm for each encountered subproblem. In this paper we identify a feature space that captures both the evolution of the problem in the branching tree and the similarity among subproblems of instances from the same MIP models. We show how to exploit these features to decide the best time to switch the branching heuristic and then show how such a system can be trained efficiently. Experiments on a highly heterogeneous collection of MIP instances show significant gains over the pure algorithm selection approach that for a given instance uses only a single heuristic throughout the search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge