Barry Hurley
Elastic Solver: Balancing Solution Time and Energy Consumption
May 23, 2016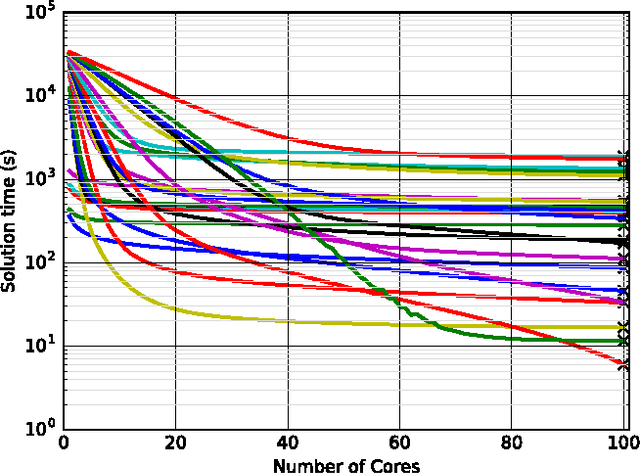
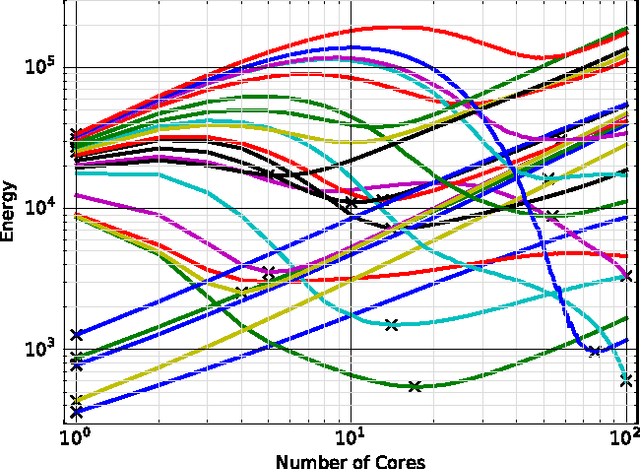
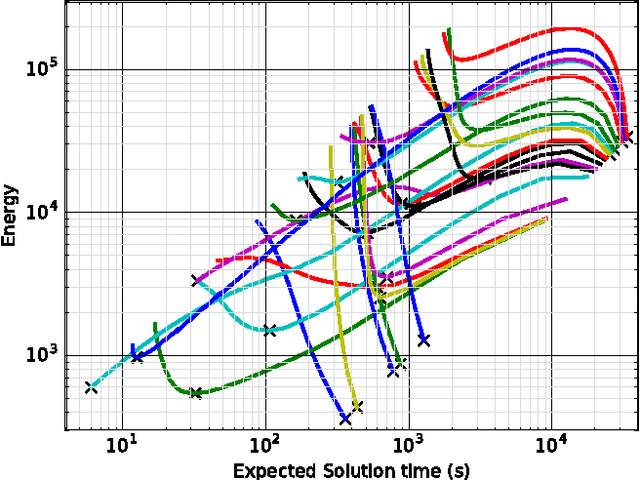
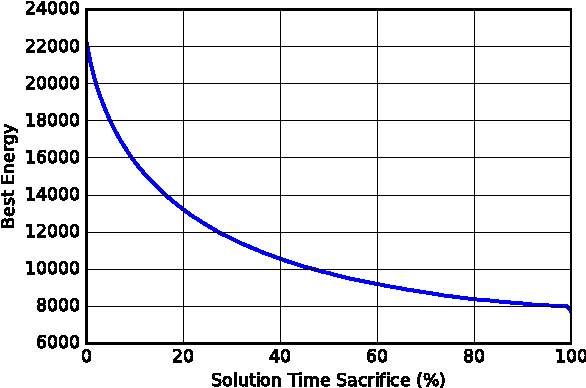
Abstract:Combinatorial decision problems arise in many different domains such as scheduling, routing, packing, bioinformatics, and many more. Despite recent advances in developing scalable solvers, there are still many problems which are often very hard to solve. Typically the most advanced solvers include elements which are stochastic in nature. If a same instance is solved many times using different seeds then depending on the inherent characteristics of a problem instance and the solver, one can observe a highly-variant distribution of times spanning multiple orders of magnitude. Therefore, to solve a problem instance efficiently it is often useful to solve the same instance in parallel with different seeds. With the proliferation of cloud computing, it is natural to think about an elastic solver which can scale up by launching searches in parallel on thousands of machines (or cores). However, this could result in consuming a lot of energy. Moreover, not every instance would require thousands of machines. The challenge is to resolve the tradeoff between solution time and energy consumption optimally for a given problem instance. We analyse the impact of the number of machines (or cores) on not only solution time but also on energy consumption. We highlight that although solution time always drops as the number of machines increases, the relation between the number of machines and energy consumption is more complicated. In many cases, the optimal energy consumption may be achieved by a middle ground, we analyse this relationship in detail. The tradeoff between solution time and energy consumption is studied further, showing that the energy consumption of a solver can be reduced drastically if we increase the solution time marginally. We also develop a prediction model, demonstrating that such insights can be exploited to achieve faster solutions times in a more energy efficient manor.
Proteus: A Hierarchical Portfolio of Solvers and Transformations
Feb 17, 2014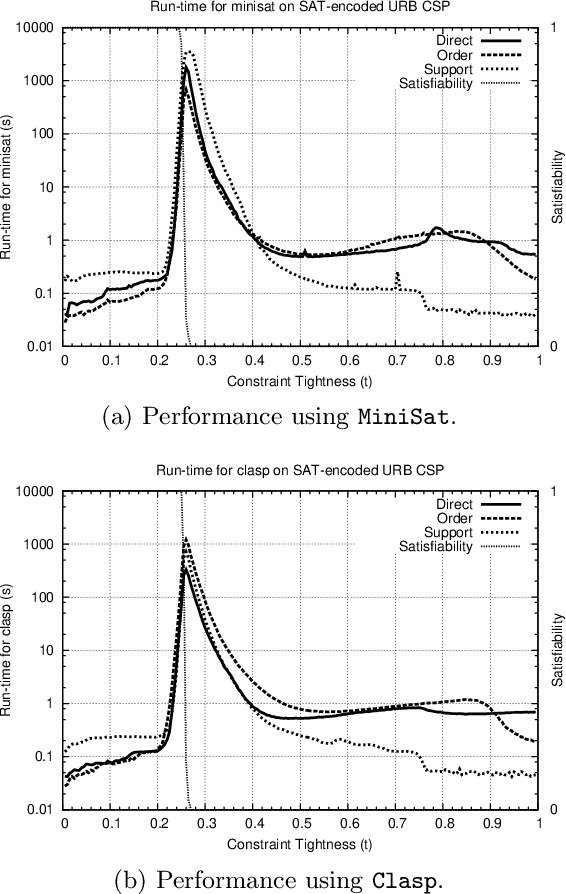
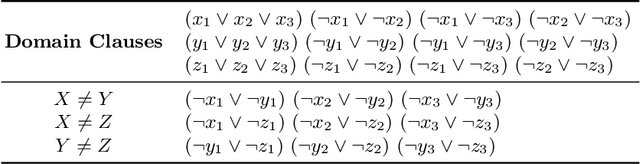
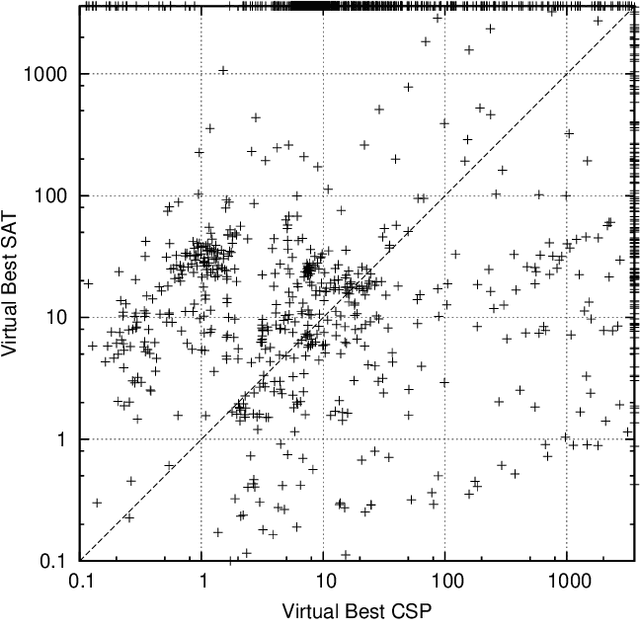
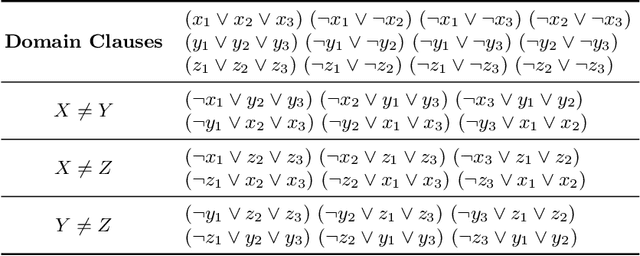
Abstract:In recent years, portfolio approaches to solving SAT problems and CSPs have become increasingly common. There are also a number of different encodings for representing CSPs as SAT instances. In this paper, we leverage advances in both SAT and CSP solving to present a novel hierarchical portfolio-based approach to CSP solving, which we call Proteus, that does not rely purely on CSP solvers. Instead, it may decide that it is best to encode a CSP problem instance into SAT, selecting an appropriate encoding and a corresponding SAT solver. Our experimental evaluation used an instance of Proteus that involved four CSP solvers, three SAT encodings, and six SAT solvers, evaluated on the most challenging problem instances from the CSP solver competitions, involving global and intensional constraints. We show that significant performance improvements can be achieved by Proteus obtained by exploiting alternative view-points and solvers for combinatorial problem-solving.
Transformation-based Feature Computation for Algorithm Portfolios
Jan 10, 2014
Abstract:Instance-specific algorithm configuration and algorithm portfolios have been shown to offer significant improvements over single algorithm approaches in a variety of application domains. In the SAT and CSP domains algorithm portfolios have consistently dominated the main competitions in these fields for the past five years. For a portfolio approach to be effective there are two crucial conditions that must be met. First, there needs to be a collection of complementary solvers with which to make a portfolio. Second, there must be a collection of problem features that can accurately identify structural differences between instances. This paper focuses on the latter issue: feature representation, because, unlike SAT, not every problem has well-studied features. We employ the well-known SATzilla feature set, but compute alternative sets on different SAT encodings of CSPs. We show that regardless of what encoding is used to convert the instances, adequate structural information is maintained to differentiate between problem instances, and that this can be exploited to make an effective portfolio-based CSP solver.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge