Elastic Solver: Balancing Solution Time and Energy Consumption
Paper and Code
May 23, 2016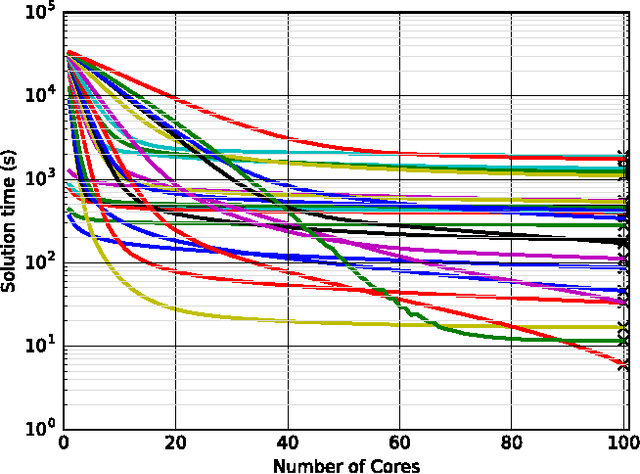
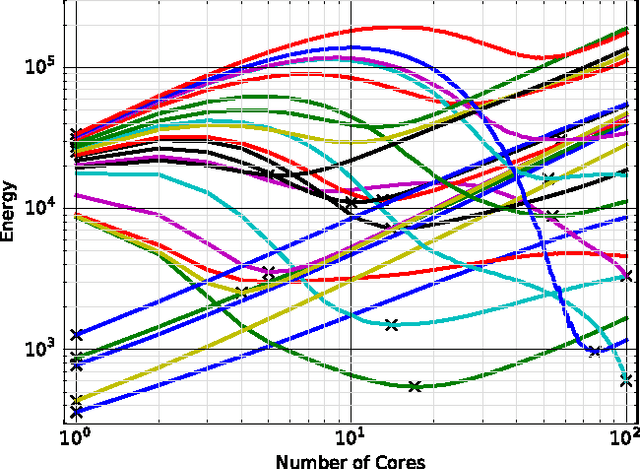
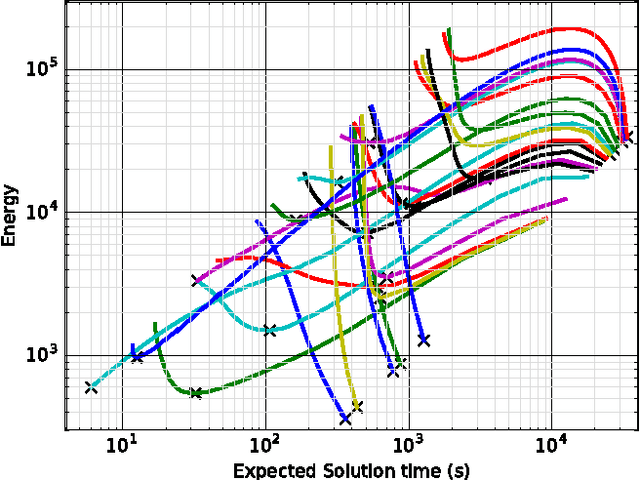
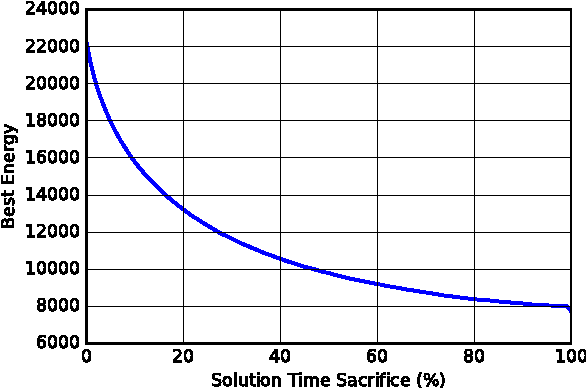
Combinatorial decision problems arise in many different domains such as scheduling, routing, packing, bioinformatics, and many more. Despite recent advances in developing scalable solvers, there are still many problems which are often very hard to solve. Typically the most advanced solvers include elements which are stochastic in nature. If a same instance is solved many times using different seeds then depending on the inherent characteristics of a problem instance and the solver, one can observe a highly-variant distribution of times spanning multiple orders of magnitude. Therefore, to solve a problem instance efficiently it is often useful to solve the same instance in parallel with different seeds. With the proliferation of cloud computing, it is natural to think about an elastic solver which can scale up by launching searches in parallel on thousands of machines (or cores). However, this could result in consuming a lot of energy. Moreover, not every instance would require thousands of machines. The challenge is to resolve the tradeoff between solution time and energy consumption optimally for a given problem instance. We analyse the impact of the number of machines (or cores) on not only solution time but also on energy consumption. We highlight that although solution time always drops as the number of machines increases, the relation between the number of machines and energy consumption is more complicated. In many cases, the optimal energy consumption may be achieved by a middle ground, we analyse this relationship in detail. The tradeoff between solution time and energy consumption is studied further, showing that the energy consumption of a solver can be reduced drastically if we increase the solution time marginally. We also develop a prediction model, demonstrating that such insights can be exploited to achieve faster solutions times in a more energy efficient manor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge