Multi-task Representation Learning for Mixed Integer Linear Programming

Mixed Integer Linear Programs (MILPs) are highly flexible and powerful tools for modeling and solving complex real-world combinatorial optimization problems. Recently, machine learning (ML)-guided approaches have demonstrated significant potential in improving MILP-solving efficiency. However, these methods typically rely on separate offline data collection and training processes, which limits their scalability and adaptability. This paper introduces the first multi-task learning framework for ML-guided MILP solving. The proposed framework provides MILP embeddings helpful in guiding MILP solving across solvers (e.g., Gurobi and SCIP) and across tasks (e.g., Branching and Solver configuration). Through extensive experiments on three widely used MILP benchmarks, we demonstrate that our multi-task learning model performs similarly to specialized models within the same distribution. Moreover, it significantly outperforms them in generalization across problem sizes and tasks.

Distributional MIPLIB: a Multi-Domain Library for Advancing ML-Guided MILP Methods

Mixed Integer Linear Programming (MILP) is a fundamental tool for modeling combinatorial optimization problems. Recently, a growing body of research has used machine learning to accelerate MILP solving. Despite the increasing popularity of this approach, there is a lack of a common repository that provides distributions of similar MILP instances across different domains, at different hardness levels, with standardized test sets. In this paper, we introduce Distributional MIPLIB, a multi-domain library of problem distributions for advancing ML-guided MILP methods. We curate MILP distributions from existing work in this area as well as real-world problems that have not been used, and classify them into different hardness levels. It will facilitate research in this area by enabling comprehensive evaluation on diverse and realistic domains. We empirically illustrate the benefits of using Distributional MIPLIB as a research vehicle in two ways. We evaluate the performance of ML-guided variable branching on previously unused distributions to identify potential areas for improvement. Moreover, we propose to learn branching policies from a mix of distributions, demonstrating that mixed distributions achieve better performance compared to homogeneous distributions when there is limited data and generalize well to larger instances.

Learning Backdoors for Mixed Integer Programs with Contrastive Learning

Many real-world problems can be efficiently modeled as Mixed Integer Programs (MIPs) and solved with the Branch-and-Bound method. Prior work has shown the existence of MIP backdoors, small sets of variables such that prioritizing branching on them when possible leads to faster running times. However, finding high-quality backdoors that improve running times remains an open question. Previous work learns to estimate the relative solver speed of randomly sampled backdoors through ranking and then decide whether to use it. In this paper, we utilize the Monte-Carlo tree search method to collect backdoors for training, rather than relying on random sampling, and adapt a contrastive learning framework to train a Graph Attention Network model to predict backdoors. Our method, evaluated on four common MIP problem domains, demonstrates performance improvements over both Gurobi and previous models.

Adaptive Anytime Multi-Agent Path Finding Using Bandit-Based Large Neighborhood Search

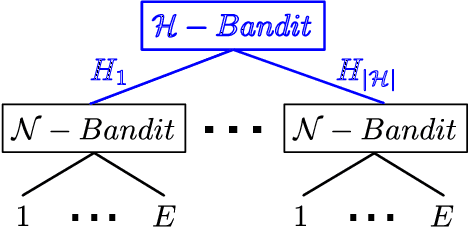
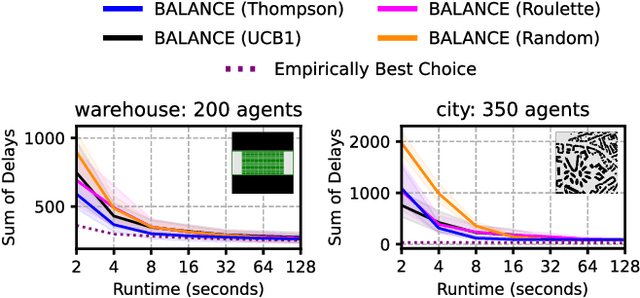
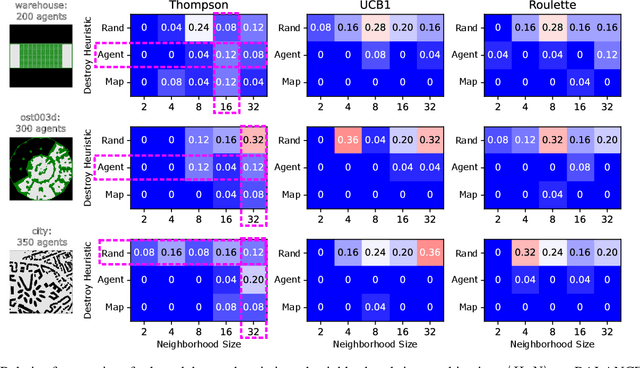
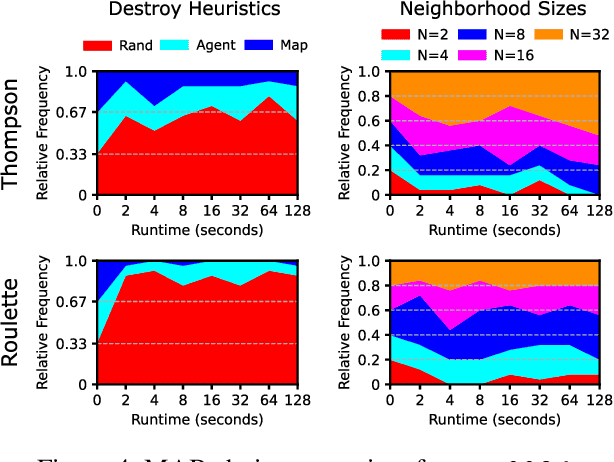
Anytime multi-agent path finding (MAPF) is a promising approach to scalable path optimization in large-scale multi-agent systems. State-of-the-art anytime MAPF is based on Large Neighborhood Search (LNS), where a fast initial solution is iteratively optimized by destroying and repairing a fixed number of parts, i.e., the neighborhood, of the solution, using randomized destroy heuristics and prioritized planning. Despite their recent success in various MAPF instances, current LNS-based approaches lack exploration and flexibility due to greedy optimization with a fixed neighborhood size which can lead to low quality solutions in general. So far, these limitations have been addressed with extensive prior effort in tuning or offline machine learning beyond actual planning. In this paper, we focus on online learning in LNS and propose Bandit-based Adaptive LArge Neighborhood search Combined with Exploration (BALANCE). BALANCE uses a bi-level multi-armed bandit scheme to adapt the selection of destroy heuristics and neighborhood sizes on the fly during search. We evaluate BALANCE on multiple maps from the MAPF benchmark set and empirically demonstrate cost improvements of at least 50% compared to state-of-the-art anytime MAPF in large-scale scenarios. We find that Thompson Sampling performs particularly well compared to alternative multi-armed bandit algorithms.

GenCO: Generating Diverse Solutions to Design Problems with Combinatorial Nature

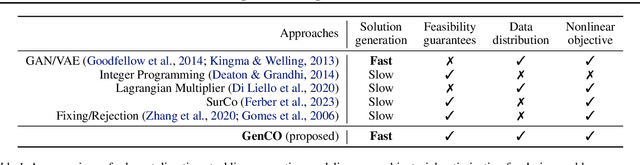
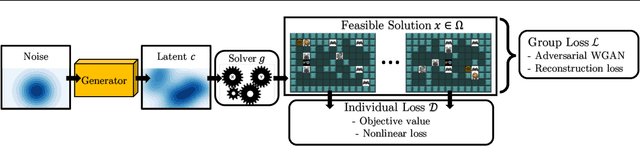
Generating diverse objects (e.g., images) using generative models (such as GAN or VAE) has achieved impressive results in the recent years, to help solve many design problems that are traditionally done by humans. Going beyond image generation, we aim to find solutions to more general design problems, in which both the diversity of the design and conformity of constraints are important. Such a setting has applications in computer graphics, animation, industrial design, material science, etc, in which we may want the output of the generator to follow discrete/combinatorial constraints and penalize any deviation, which is non-trivial with existing generative models and optimization solvers. To address this, we propose GenCO, a novel framework that conducts end-to-end training of deep generative models integrated with embedded combinatorial solvers, aiming to uncover high-quality solutions aligned with nonlinear objectives. While structurally akin to conventional generative models, GenCO diverges in its role - it focuses on generating instances of combinatorial optimization problems rather than final objects (e.g., images). This shift allows finer control over the generated outputs, enabling assessments of their feasibility and introducing an additional combinatorial loss component. We demonstrate the effectiveness of our approach on a variety of generative tasks characterized by combinatorial intricacies, including game level generation and map creation for path planning, consistently demonstrating its capability to yield diverse, high-quality solutions that reliably adhere to user-specified combinatorial properties.

Landscape Surrogate: Learning Decision Losses for Mathematical Optimization Under Partial Information

Recent works in learning-integrated optimization have shown promise in settings where the optimization problem is only partially observed or where general-purpose optimizers perform poorly without expert tuning. By learning an optimizer $\mathbf{g}$ to tackle these challenging problems with $f$ as the objective, the optimization process can be substantially accelerated by leveraging past experience. The optimizer can be trained with supervision from known optimal solutions or implicitly by optimizing the compound function $f\circ \mathbf{g}$. The implicit approach may not require optimal solutions as labels and is capable of handling problem uncertainty; however, it is slow to train and deploy due to frequent calls to optimizer $\mathbf{g}$ during both training and testing. The training is further challenged by sparse gradients of $\mathbf{g}$, especially for combinatorial solvers. To address these challenges, we propose using a smooth and learnable Landscape Surrogate $M$ as a replacement for $f\circ \mathbf{g}$. This surrogate, learnable by neural networks, can be computed faster than the solver $\mathbf{g}$, provides dense and smooth gradients during training, can generalize to unseen optimization problems, and is efficiently learned via alternating optimization. We test our approach on both synthetic problems, including shortest path and multidimensional knapsack, and real-world problems such as portfolio optimization, achieving comparable or superior objective values compared to state-of-the-art baselines while reducing the number of calls to $\mathbf{g}$. Notably, our approach outperforms existing methods for computationally expensive high-dimensional problems.

Searching Large Neighborhoods for Integer Linear Programs with Contrastive Learning

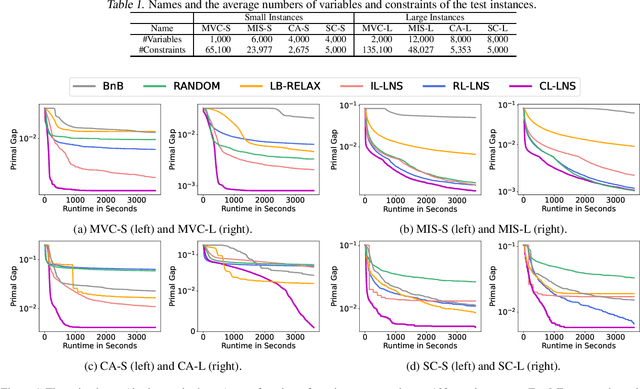
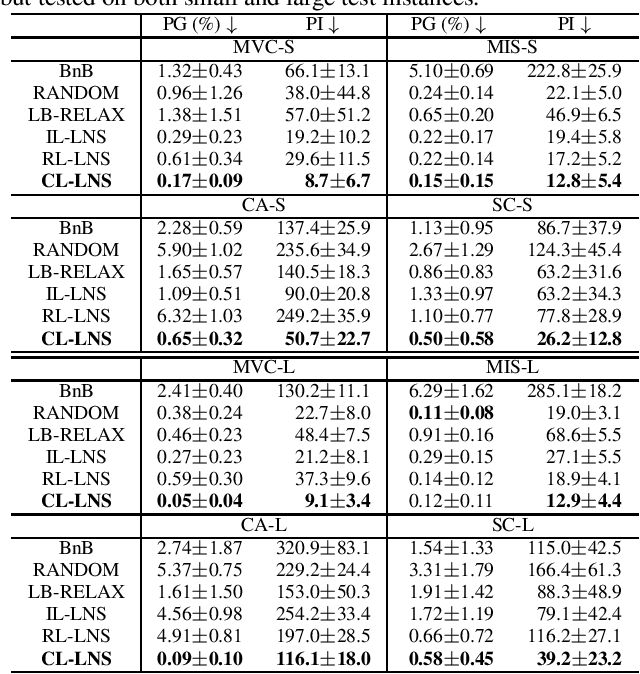
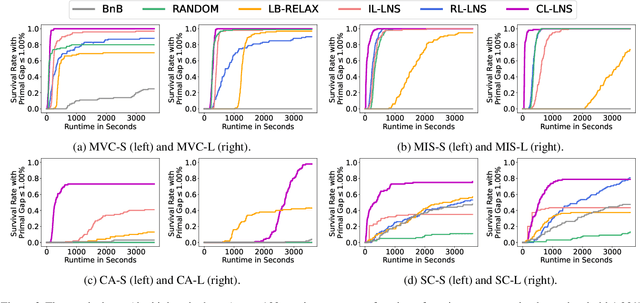
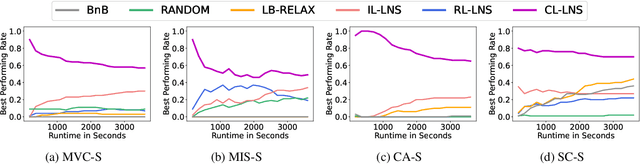
Integer Linear Programs (ILPs) are powerful tools for modeling and solving a large number of combinatorial optimization problems. Recently, it has been shown that Large Neighborhood Search (LNS), as a heuristic algorithm, can find high quality solutions to ILPs faster than Branch and Bound. However, how to find the right heuristics to maximize the performance of LNS remains an open problem. In this paper, we propose a novel approach, CL-LNS, that delivers state-of-the-art anytime performance on several ILP benchmarks measured by metrics including the primal gap, the primal integral, survival rates and the best performing rate. Specifically, CL-LNS collects positive and negative solution samples from an expert heuristic that is slow to compute and learns a new one with a contrastive loss. We use graph attention networks and a richer set of features to further improve its performance.

Local Branching Relaxation Heuristics for Integer Linear Programs

Large Neighborhood Search (LNS) is a popular heuristic algorithm for solving combinatorial optimization problems (COP). It starts with an initial solution to the problem and iteratively improves it by searching a large neighborhood around the current best solution. LNS relies on heuristics to select neighborhoods to search in. In this paper, we focus on designing effective and efficient heuristics in LNS for integer linear programs (ILP) since a wide range of COPs can be represented as ILPs. Local Branching (LB) is a heuristic that selects the neighborhood that leads to the largest improvement over the current solution in each iteration of LNS. LB is often slow since it needs to solve an ILP of the same size as input. Our proposed heuristics, LB-RELAX and its variants, use the linear programming relaxation of LB to select neighborhoods. Empirically, LB-RELAX and its variants compute as effective neighborhoods as LB but run faster. They achieve state-of-the-art anytime performance on several ILP benchmarks.

SurCo: Learning Linear Surrogates For Combinatorial Nonlinear Optimization Problems

Optimization problems with expensive nonlinear cost functions and combinatorial constraints appear in many real-world applications, but remain challenging to solve efficiently. Existing combinatorial solvers like Mixed Integer Linear Programming can be fast in practice but cannot readily optimize nonlinear cost functions, while general nonlinear optimizers like gradient descent often do not handle complex combinatorial structures, may require many queries of the cost function, and are prone to local optima. To bridge this gap, we propose SurCo that learns linear Surrogate costs which can be used by existing Combinatorial solvers to output good solutions to the original nonlinear combinatorial optimization problem, combining the flexibility of gradient-based methods with the structure of linear combinatorial optimization. We learn these linear surrogates end-to-end with the nonlinear loss by differentiating through the linear surrogate solver. Three variants of SurCo are proposed: SurCo-zero operates on individual nonlinear problems, SurCo-prior trains a linear surrogate predictor on distributions of problems, and SurCo-hybrid uses a model trained offline to warm start online solving for SurCo-zero. We analyze our method theoretically and empirically, showing smooth convergence and improved performance. Experiments show that compared to state-of-the-art approaches and expert-designed heuristics, SurCo obtains lower cost solutions with comparable or faster solve time for two realworld industry-level applications: embedding table sharding and inverse photonic design.

The (Un)Scalability of Heuristic Approximators for NP-Hard Search Problems

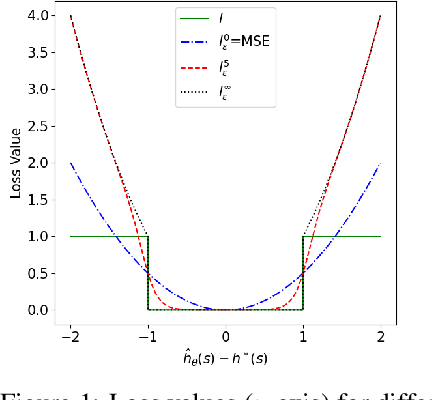
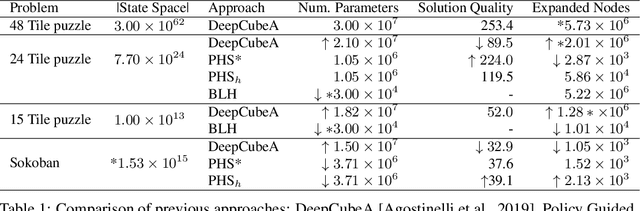
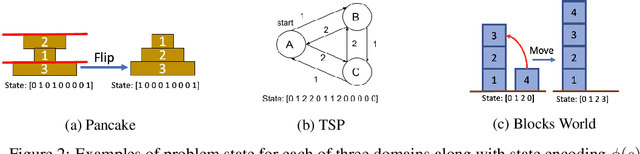
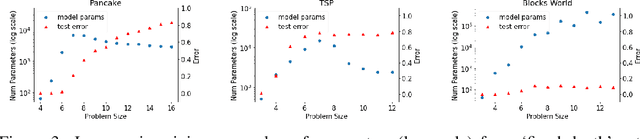
The A* algorithm is commonly used to solve NP-hard combinatorial optimization problems. When provided with an accurate heuristic function, A* can solve such problems in time complexity that is polynomial in the solution depth. This fact implies that accurate heuristic approximation for many such problems is also NP-hard. In this context, we examine a line of recent publications that propose the use of deep neural networks for heuristic approximation. We assert that these works suffer from inherent scalability limitations since -- under the assumption that P$\ne$NP -- such approaches result in either (a) network sizes that scale exponentially in the instance sizes or (b) heuristic approximation accuracy that scales inversely with the instance sizes. Our claim is supported by experimental results for three representative NP-hard search problems that show that fitting deep neural networks accurately to heuristic functions necessitates network sizes that scale exponentially with the instance size.