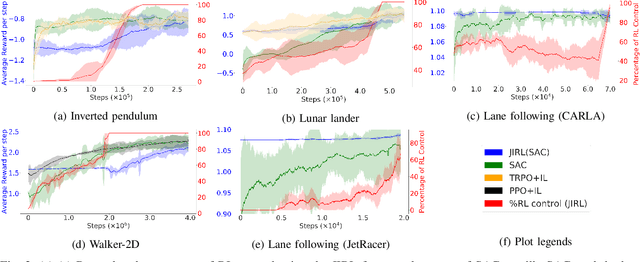
A Joint Imitation-Reinforcement Learning Framework for Reduced Baseline Regret

In various control task domains, existing controllers provide a baseline level of performance that -- though possibly suboptimal -- should be maintained. Reinforcement learning (RL) algorithms that rely on extensive exploration of the state and action space can be used to optimize a control policy. However, fully exploratory RL algorithms may decrease performance below a baseline level during training. In this paper, we address the issue of online optimization of a control policy while minimizing regret w.r.t a baseline policy performance. We present a joint imitation-reinforcement learning framework, denoted JIRL. The learning process in JIRL assumes the availability of a baseline policy and is designed with two objectives in mind \textbf{(a)} leveraging the baseline's online demonstrations to minimize the regret w.r.t the baseline policy during training, and \textbf{(b)} eventually surpassing the baseline performance. JIRL addresses these objectives by initially learning to imitate the baseline policy and gradually shifting control from the baseline to an RL agent. Experimental results show that JIRL effectively accomplishes the aforementioned objectives in several, continuous action-space domains. The results demonstrate that JIRL is comparable to a state-of-the-art algorithm in its final performance while incurring significantly lower baseline regret during training in all of the presented domains. Moreover, the results show a reduction factor of up to $21$ in baseline regret over a state-of-the-art baseline regret minimization approach.

The (Un)Scalability of Heuristic Approximators for NP-Hard Search Problems

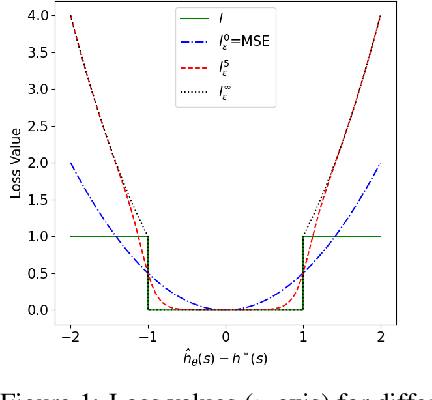
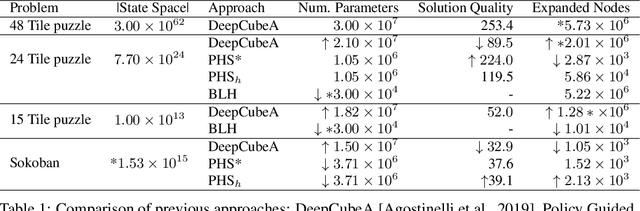
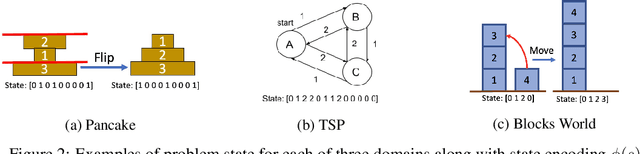
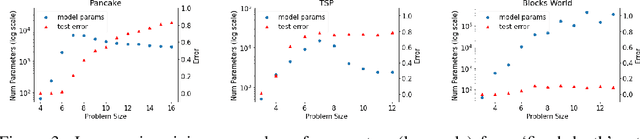
The A* algorithm is commonly used to solve NP-hard combinatorial optimization problems. When provided with an accurate heuristic function, A* can solve such problems in time complexity that is polynomial in the solution depth. This fact implies that accurate heuristic approximation for many such problems is also NP-hard. In this context, we examine a line of recent publications that propose the use of deep neural networks for heuristic approximation. We assert that these works suffer from inherent scalability limitations since -- under the assumption that P$\ne$NP -- such approaches result in either (a) network sizes that scale exponentially in the instance sizes or (b) heuristic approximation accuracy that scales inversely with the instance sizes. Our claim is supported by experimental results for three representative NP-hard search problems that show that fitting deep neural networks accurately to heuristic functions necessitates network sizes that scale exponentially with the instance size.