User-Centric Cell-Free Wireless Networks for 6G: Communication Theoretic Models and Research Challenges

This paper presents a comprehensive communication theoretic model for the physical layer of a cell-free user-centric network, formed by user equipments (UEs), radio units (RUs), and decentralized units (DUs), uniformly spatially distributed over a given coverage area. We consider RUs equipped with multiple antennas, and focus on the regime where the UE, RU, and DU densities are constant and therefore the number of such nodes grows with the coverage area. A system is said scalable if the computing load and information rate at any node in the network converges to a constant as the network size (coverage area) grows to infinity. This imposes that each UE must be processed by a (user-centric) finite-size cluster of RUs, and that such cluster processors are dynamically allocated to the DUs (e.g., as software defined virtual network functions) in order to achieve a balanced computation load. We also assume that the RUs are connected to the DUs through a packet switching network, in order to achieve adaptive routing and load balance. For this model, we define in details the dynamic cluster formation and uplink pilot allocation. As a consequence of the pilot allocation and the scalability constraint, each cluster processor has a partial view of the network channel state information. We define the condition of ``ideal partial CSI'' when the channel vectors that can be estimated are perfectly known (while the ones that cannot be estimated are not know at all). We develop two attractive cluster-based linear receiver schemes for the uplink, and an uplink-downlink duality that allows to reuse such vectors as precoders for the downlink.

SurCo: Learning Linear Surrogates For Combinatorial Nonlinear Optimization Problems

Optimization problems with expensive nonlinear cost functions and combinatorial constraints appear in many real-world applications, but remain challenging to solve efficiently. Existing combinatorial solvers like Mixed Integer Linear Programming can be fast in practice but cannot readily optimize nonlinear cost functions, while general nonlinear optimizers like gradient descent often do not handle complex combinatorial structures, may require many queries of the cost function, and are prone to local optima. To bridge this gap, we propose SurCo that learns linear Surrogate costs which can be used by existing Combinatorial solvers to output good solutions to the original nonlinear combinatorial optimization problem, combining the flexibility of gradient-based methods with the structure of linear combinatorial optimization. We learn these linear surrogates end-to-end with the nonlinear loss by differentiating through the linear surrogate solver. Three variants of SurCo are proposed: SurCo-zero operates on individual nonlinear problems, SurCo-prior trains a linear surrogate predictor on distributions of problems, and SurCo-hybrid uses a model trained offline to warm start online solving for SurCo-zero. We analyze our method theoretically and empirically, showing smooth convergence and improved performance. Experiments show that compared to state-of-the-art approaches and expert-designed heuristics, SurCo obtains lower cost solutions with comparable or faster solve time for two realworld industry-level applications: embedding table sharding and inverse photonic design.

Closed-form max-min power control for some cellular and cell-free massive MIMO networks

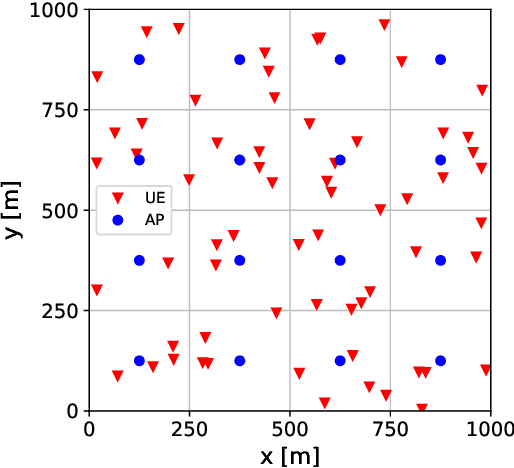
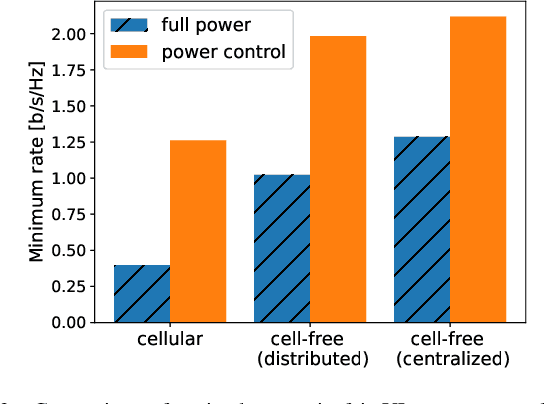
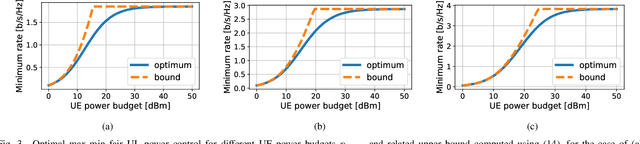
Many common instances of power control problems for cellular and cell-free massive MIMO networks can be interpreted as max-min utility optimization problems involving affine interference mappings and polyhedral constraints. We show that these problems admit a closed-form solution which depends on the spectral radius of known matrices. In contrast, previous solutions in the literature have been indirectly obtained using iterative algorithms based on the bisection method, or on fixed-point iterations. Furthermore, we also show an asymptotically tight bound for the optimal utility, which in turn provides a simple rule of thumb for evaluating whether the network is operating in the noise or interference limited regime. We finally illustrate our results by focusing on classical max-min fair power control for cell-free massive MIMO networks.