Closed-form max-min power control for some cellular and cell-free massive MIMO networks
Paper and Code
May 03, 2022
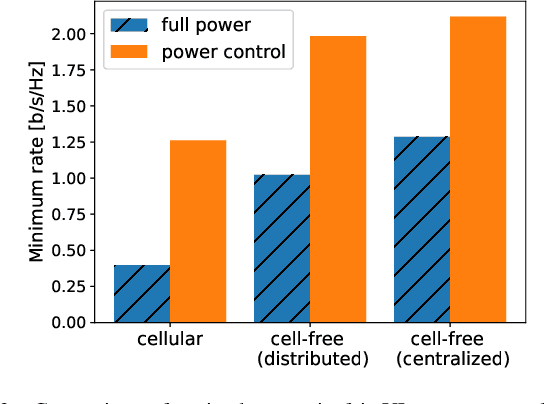
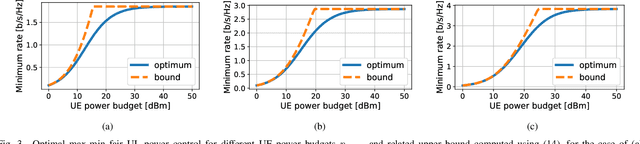
Many common instances of power control problems for cellular and cell-free massive MIMO networks can be interpreted as max-min utility optimization problems involving affine interference mappings and polyhedral constraints. We show that these problems admit a closed-form solution which depends on the spectral radius of known matrices. In contrast, previous solutions in the literature have been indirectly obtained using iterative algorithms based on the bisection method, or on fixed-point iterations. Furthermore, we also show an asymptotically tight bound for the optimal utility, which in turn provides a simple rule of thumb for evaluating whether the network is operating in the noise or interference limited regime. We finally illustrate our results by focusing on classical max-min fair power control for cell-free massive MIMO networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge