Optimal Beamforming for Bistatic MIMO Sensing

This paper considers the beamforming optimization for sensing a point-like scatterer using a bistatic multiple-input multiple-output (MIMO) orthogonal frequency-division multiplexing (OFDM) radar, which could be part of a joint communication and sensing system. The goal is to minimize the Cram\'er-Rao bound on the target position's estimation error, where the radar already knows an approximate position that is taken into account in the optimization. The optimization allows for beamforming with more than one beam per subcarrier. Optimal solutions for the beamforming are discussed for known and unknown channel gain. Numerical results show that beamforming with at most one beam per subcarrier is optimal for certain parameters, but for other parameters, optimal solutions need two beams on some subcarriers. In addition, the degree of freedom in selecting which end of the bistatic radar should transmit and receive is considered.

Closed-form max-min power control for some cellular and cell-free massive MIMO networks

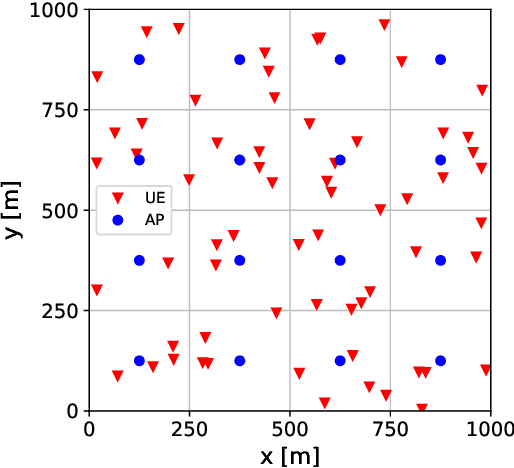
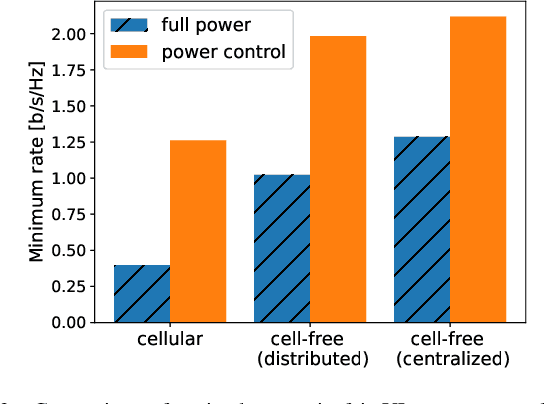
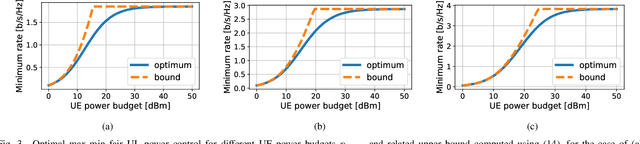
Many common instances of power control problems for cellular and cell-free massive MIMO networks can be interpreted as max-min utility optimization problems involving affine interference mappings and polyhedral constraints. We show that these problems admit a closed-form solution which depends on the spectral radius of known matrices. In contrast, previous solutions in the literature have been indirectly obtained using iterative algorithms based on the bisection method, or on fixed-point iterations. Furthermore, we also show an asymptotically tight bound for the optimal utility, which in turn provides a simple rule of thumb for evaluating whether the network is operating in the noise or interference limited regime. We finally illustrate our results by focusing on classical max-min fair power control for cell-free massive MIMO networks.