AiSciVision: A Framework for Specializing Large Multimodal Models in Scientific Image Classification

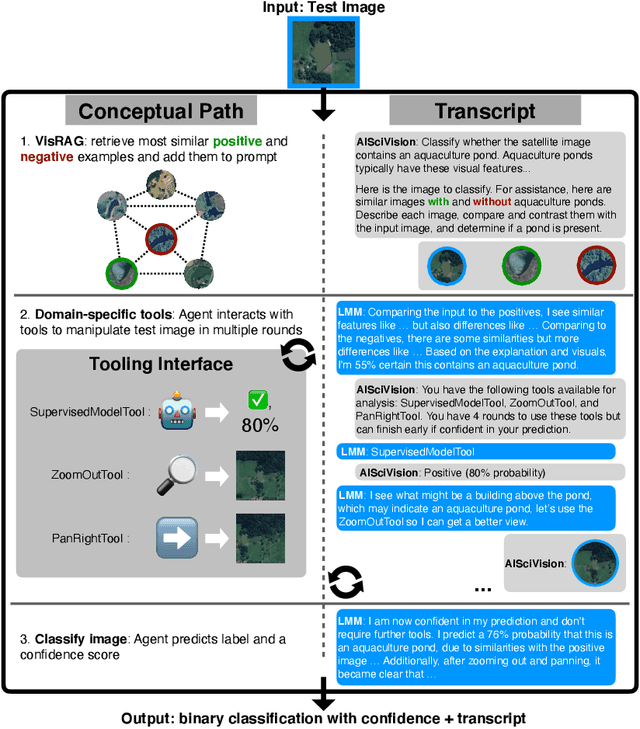
Trust and interpretability are crucial for the use of Artificial Intelligence (AI) in scientific research, but current models often operate as black boxes offering limited transparency and justifications for their outputs. We introduce AiSciVision, a framework that specializes Large Multimodal Models (LMMs) into interactive research partners and classification models for image classification tasks in niche scientific domains. Our framework uses two key components: (1) Visual Retrieval-Augmented Generation (VisRAG) and (2) domain-specific tools utilized in an agentic workflow. To classify a target image, AiSciVision first retrieves the most similar positive and negative labeled images as context for the LMM. Then the LMM agent actively selects and applies tools to manipulate and inspect the target image over multiple rounds, refining its analysis before making a final prediction. These VisRAG and tooling components are designed to mirror the processes of domain experts, as humans often compare new data to similar examples and use specialized tools to manipulate and inspect images before arriving at a conclusion. Each inference produces both a prediction and a natural language transcript detailing the reasoning and tool usage that led to the prediction. We evaluate AiSciVision on three real-world scientific image classification datasets: detecting the presence of aquaculture ponds, diseased eelgrass, and solar panels. Across these datasets, our method outperforms fully supervised models in low and full-labeled data settings. AiSciVision is actively deployed in real-world use, specifically for aquaculture research, through a dedicated web application that displays and allows the expert users to converse with the transcripts. This work represents a crucial step toward AI systems that are both interpretable and effective, advancing their use in scientific research and scientific discovery.

Diffusion Models as Constrained Samplers for Optimization with Unknown Constraints

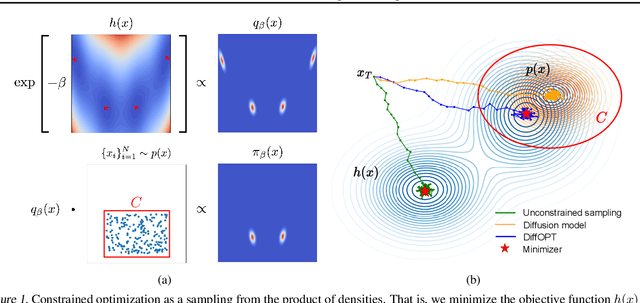
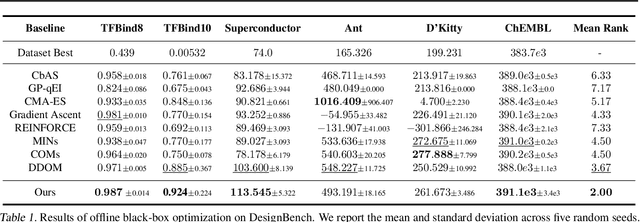
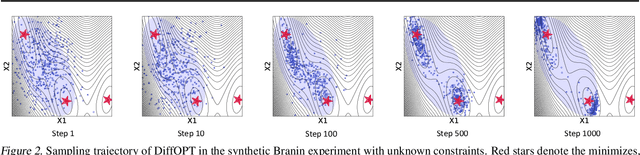
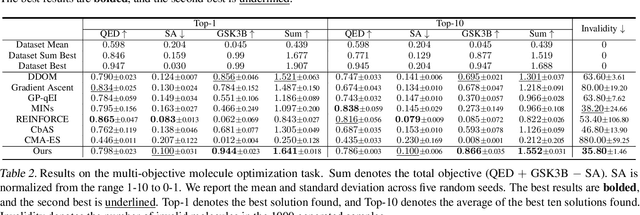
Addressing real-world optimization problems becomes particularly challenging when analytic objective functions or constraints are unavailable. While numerous studies have addressed the issue of unknown objectives, limited research has focused on scenarios where feasibility constraints are not given explicitly. Overlooking these constraints can lead to spurious solutions that are unrealistic in practice. To deal with such unknown constraints, we propose to perform optimization within the data manifold using diffusion models. To constrain the optimization process to the data manifold, we reformulate the original optimization problem as a sampling problem from the product of the Boltzmann distribution defined by the objective function and the data distribution learned by the diffusion model. To enhance sampling efficiency, we propose a two-stage framework that begins with a guided diffusion process for warm-up, followed by a Langevin dynamics stage for further correction. Theoretical analysis shows that the initial stage results in a distribution focused on feasible solutions, thereby providing a better initialization for the later stage. Comprehensive experiments on a synthetic dataset, six real-world black-box optimization datasets, and a multi-objective optimization dataset show that our method achieves better or comparable performance with previous state-of-the-art baselines.

Learning Lagrangian Multipliers for the Travelling Salesman Problem

Lagrangian relaxation is a versatile mathematical technique employed to relax constraints in an optimization problem, enabling the generation of dual bounds to prove the optimality of feasible solutions and the design of efficient propagators in constraint programming (such as the weighted circuit constraint). However, the conventional process of deriving Lagrangian multipliers (e.g., using subgradient methods) is often computationally intensive, limiting its practicality for large-scale or time-sensitive problems. To address this challenge, we propose an innovative unsupervised learning approach that harnesses the capabilities of graph neural networks to exploit the problem structure, aiming to generate accurate Lagrangian multipliers efficiently. We apply this technique to the well-known Held-Karp Lagrangian relaxation for the travelling salesman problem. The core idea is to predict accurate Lagrangian multipliers and to employ them as a warm start for generating Held-Karp relaxation bounds. These bounds are subsequently utilized to enhance the filtering process carried out by branch-and-bound algorithms. In contrast to much of the existing literature, which primarily focuses on finding feasible solutions, our approach operates on the dual side, demonstrating that learning can also accelerate the proof of optimality. We conduct experiments across various distributions of the metric travelling salesman problem, considering instances with up to 200 cities. The results illustrate that our approach can improve the filtering level of the weighted circuit global constraint, reduce the optimality gap by a factor two for unsolved instances up to a timeout, and reduce the execution time for solved instances by 10%.

GenCO: Generating Diverse Solutions to Design Problems with Combinatorial Nature

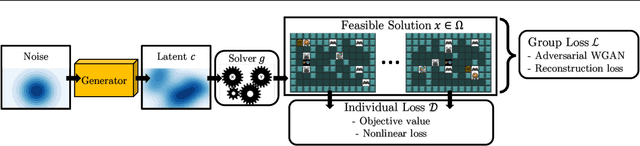
Generating diverse objects (e.g., images) using generative models (such as GAN or VAE) has achieved impressive results in the recent years, to help solve many design problems that are traditionally done by humans. Going beyond image generation, we aim to find solutions to more general design problems, in which both the diversity of the design and conformity of constraints are important. Such a setting has applications in computer graphics, animation, industrial design, material science, etc, in which we may want the output of the generator to follow discrete/combinatorial constraints and penalize any deviation, which is non-trivial with existing generative models and optimization solvers. To address this, we propose GenCO, a novel framework that conducts end-to-end training of deep generative models integrated with embedded combinatorial solvers, aiming to uncover high-quality solutions aligned with nonlinear objectives. While structurally akin to conventional generative models, GenCO diverges in its role - it focuses on generating instances of combinatorial optimization problems rather than final objects (e.g., images). This shift allows finer control over the generated outputs, enabling assessments of their feasibility and introducing an additional combinatorial loss component. We demonstrate the effectiveness of our approach on a variety of generative tasks characterized by combinatorial intricacies, including game level generation and map creation for path planning, consistently demonstrating its capability to yield diverse, high-quality solutions that reliably adhere to user-specified combinatorial properties.

Landscape Surrogate: Learning Decision Losses for Mathematical Optimization Under Partial Information

Recent works in learning-integrated optimization have shown promise in settings where the optimization problem is only partially observed or where general-purpose optimizers perform poorly without expert tuning. By learning an optimizer $\mathbf{g}$ to tackle these challenging problems with $f$ as the objective, the optimization process can be substantially accelerated by leveraging past experience. The optimizer can be trained with supervision from known optimal solutions or implicitly by optimizing the compound function $f\circ \mathbf{g}$. The implicit approach may not require optimal solutions as labels and is capable of handling problem uncertainty; however, it is slow to train and deploy due to frequent calls to optimizer $\mathbf{g}$ during both training and testing. The training is further challenged by sparse gradients of $\mathbf{g}$, especially for combinatorial solvers. To address these challenges, we propose using a smooth and learnable Landscape Surrogate $M$ as a replacement for $f\circ \mathbf{g}$. This surrogate, learnable by neural networks, can be computed faster than the solver $\mathbf{g}$, provides dense and smooth gradients during training, can generalize to unseen optimization problems, and is efficiently learned via alternating optimization. We test our approach on both synthetic problems, including shortest path and multidimensional knapsack, and real-world problems such as portfolio optimization, achieving comparable or superior objective values compared to state-of-the-art baselines while reducing the number of calls to $\mathbf{g}$. Notably, our approach outperforms existing methods for computationally expensive high-dimensional problems.

Searching Large Neighborhoods for Integer Linear Programs with Contrastive Learning

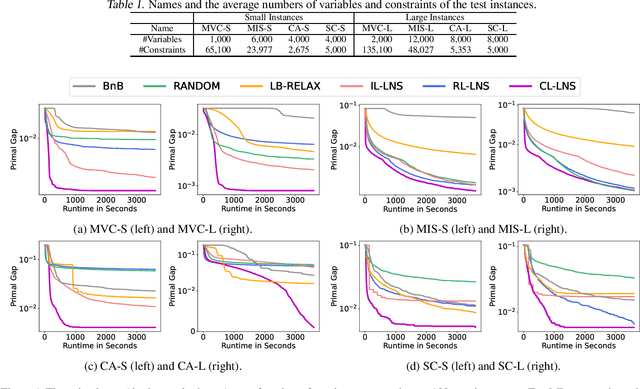
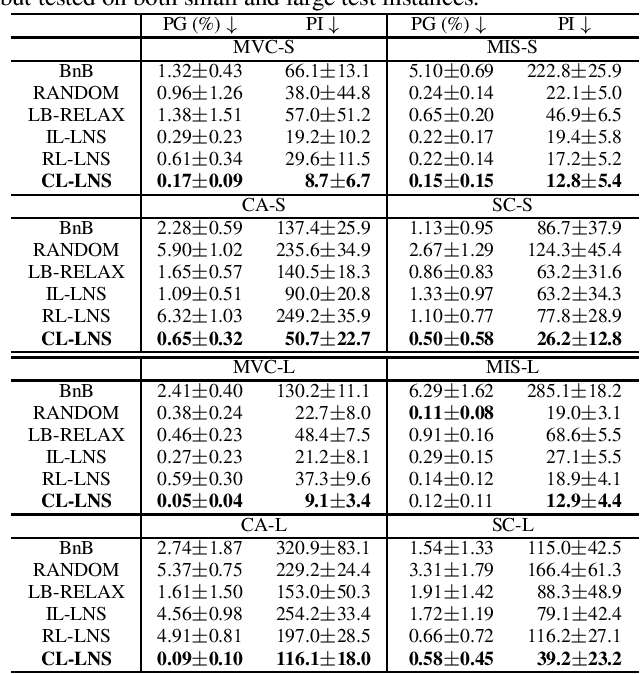
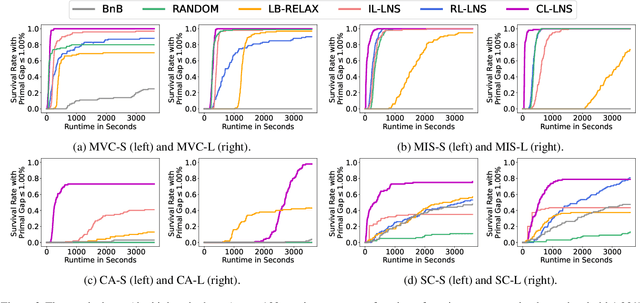
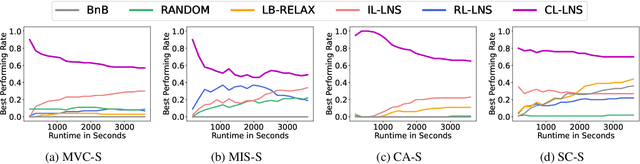
Integer Linear Programs (ILPs) are powerful tools for modeling and solving a large number of combinatorial optimization problems. Recently, it has been shown that Large Neighborhood Search (LNS), as a heuristic algorithm, can find high quality solutions to ILPs faster than Branch and Bound. However, how to find the right heuristics to maximize the performance of LNS remains an open problem. In this paper, we propose a novel approach, CL-LNS, that delivers state-of-the-art anytime performance on several ILP benchmarks measured by metrics including the primal gap, the primal integral, survival rates and the best performing rate. Specifically, CL-LNS collects positive and negative solution samples from an expert heuristic that is slow to compute and learns a new one with a contrastive loss. We use graph attention networks and a richer set of features to further improve its performance.

Local Branching Relaxation Heuristics for Integer Linear Programs

Large Neighborhood Search (LNS) is a popular heuristic algorithm for solving combinatorial optimization problems (COP). It starts with an initial solution to the problem and iteratively improves it by searching a large neighborhood around the current best solution. LNS relies on heuristics to select neighborhoods to search in. In this paper, we focus on designing effective and efficient heuristics in LNS for integer linear programs (ILP) since a wide range of COPs can be represented as ILPs. Local Branching (LB) is a heuristic that selects the neighborhood that leads to the largest improvement over the current solution in each iteration of LNS. LB is often slow since it needs to solve an ILP of the same size as input. Our proposed heuristics, LB-RELAX and its variants, use the linear programming relaxation of LB to select neighborhoods. Empirically, LB-RELAX and its variants compute as effective neighborhoods as LB but run faster. They achieve state-of-the-art anytime performance on several ILP benchmarks.

SurCo: Learning Linear Surrogates For Combinatorial Nonlinear Optimization Problems

Optimization problems with expensive nonlinear cost functions and combinatorial constraints appear in many real-world applications, but remain challenging to solve efficiently. Existing combinatorial solvers like Mixed Integer Linear Programming can be fast in practice but cannot readily optimize nonlinear cost functions, while general nonlinear optimizers like gradient descent often do not handle complex combinatorial structures, may require many queries of the cost function, and are prone to local optima. To bridge this gap, we propose SurCo that learns linear Surrogate costs which can be used by existing Combinatorial solvers to output good solutions to the original nonlinear combinatorial optimization problem, combining the flexibility of gradient-based methods with the structure of linear combinatorial optimization. We learn these linear surrogates end-to-end with the nonlinear loss by differentiating through the linear surrogate solver. Three variants of SurCo are proposed: SurCo-zero operates on individual nonlinear problems, SurCo-prior trains a linear surrogate predictor on distributions of problems, and SurCo-hybrid uses a model trained offline to warm start online solving for SurCo-zero. We analyze our method theoretically and empirically, showing smooth convergence and improved performance. Experiments show that compared to state-of-the-art approaches and expert-designed heuristics, SurCo obtains lower cost solutions with comparable or faster solve time for two realworld industry-level applications: embedding table sharding and inverse photonic design.

Learning Pseudo-Backdoors for Mixed Integer Programs

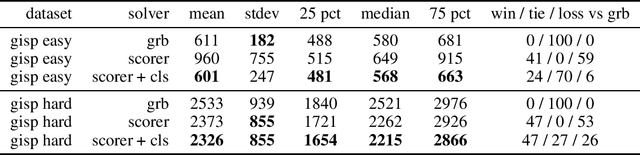
We propose a machine learning approach for quickly solving Mixed Integer Programs (MIP) by learning to prioritize a set of decision variables, which we call pseudo-backdoors, for branching that results in faster solution times. Learning-based approaches have seen success in the area of solving combinatorial optimization problems by being able to flexibly leverage common structures in a given distribution of problems. Our approach takes inspiration from the concept of strong backdoors, which corresponds to a small set of variables such that only branching on these variables yields an optimal integral solution and a proof of optimality. Our notion of pseudo-backdoors corresponds to a small set of variables such that only branching on them leads to faster solve time (which can be solver dependent). A key advantage of pseudo-backdoors over strong backdoors is that they are much amenable to data-driven identification or prediction. Our proposed method learns to estimate the solver performance of a proposed pseudo-backdoor, using a labeled dataset collected on a set of training MIP instances. This model can then be used to identify high-quality pseudo-backdoors on new MIP instances from the same distribution. We evaluate our method on the generalized independent set problems and find that our approach can efficiently identify high-quality pseudo-backdoors. In addition, we compare our learned approach against Gurobi, a state-of-the-art MIP solver, demonstrating that our method can be used to improve solver performance.

Controllable Guarantees for Fair Outcomes via Contrastive Information Estimation

Controlling bias in training datasets is vital for ensuring equal treatment, or parity, between different groups in downstream applications. A naive solution is to transform the data so that it is statistically independent of group membership, but this may throw away too much information when a reasonable compromise between fairness and accuracy is desired. Another common approach is to limit the ability of a particular adversary who seeks to maximize parity. Unfortunately, representations produced by adversarial approaches may still retain biases as their efficacy is tied to the complexity of the adversary used during training. To this end, we theoretically establish that by limiting the mutual information between representations and protected attributes, we can assuredly control the parity of any downstream classifier. We demonstrate an effective method for controlling parity through mutual information based on contrastive information estimators and show that they outperform approaches that rely on variational bounds based on complex generative models. We test our approach on UCI Adult and Heritage Health datasets and demonstrate that our approach provides more informative representations across a range of desired parity thresholds while providing strong theoretical guarantees on the parity of any downstream algorithm.