Diffusion Models as Constrained Samplers for Optimization with Unknown Constraints

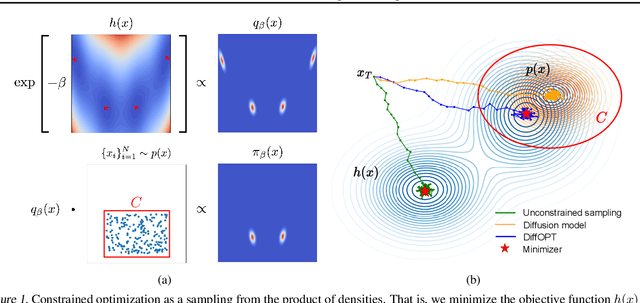
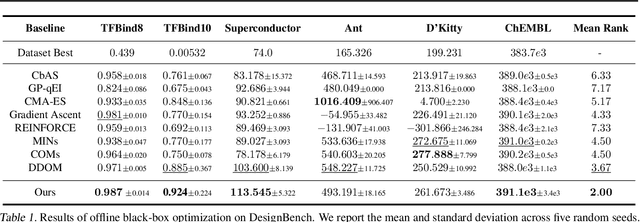
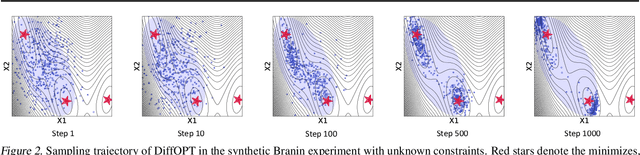
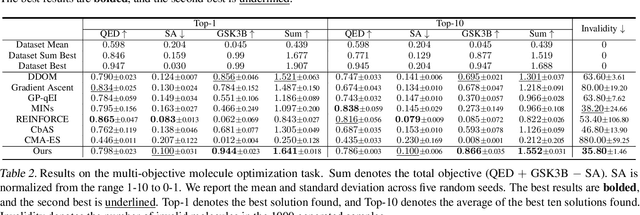
Addressing real-world optimization problems becomes particularly challenging when analytic objective functions or constraints are unavailable. While numerous studies have addressed the issue of unknown objectives, limited research has focused on scenarios where feasibility constraints are not given explicitly. Overlooking these constraints can lead to spurious solutions that are unrealistic in practice. To deal with such unknown constraints, we propose to perform optimization within the data manifold using diffusion models. To constrain the optimization process to the data manifold, we reformulate the original optimization problem as a sampling problem from the product of the Boltzmann distribution defined by the objective function and the data distribution learned by the diffusion model. To enhance sampling efficiency, we propose a two-stage framework that begins with a guided diffusion process for warm-up, followed by a Langevin dynamics stage for further correction. Theoretical analysis shows that the initial stage results in a distribution focused on feasible solutions, thereby providing a better initialization for the later stage. Comprehensive experiments on a synthetic dataset, six real-world black-box optimization datasets, and a multi-objective optimization dataset show that our method achieves better or comparable performance with previous state-of-the-art baselines.

DF2: Distribution-Free Decision-Focused Learning

Decision-focused learning (DFL) has recently emerged as a powerful approach for predict-then-optimize problems by customizing a predictive model to a downstream optimization task. However, existing end-to-end DFL methods are hindered by three significant bottlenecks: model mismatch error, sample average approximation error, and gradient approximation error. Model mismatch error stems from the misalignment between the model's parameterized predictive distribution and the true probability distribution. Sample average approximation error arises when using finite samples to approximate the expected optimization objective. Gradient approximation error occurs as DFL relies on the KKT condition for exact gradient computation, while most methods approximate the gradient for backpropagation in non-convex objectives. In this paper, we present DF2 -- the first \textit{distribution-free} decision-focused learning method explicitly designed to address these three bottlenecks. Rather than depending on a task-specific forecaster that requires precise model assumptions, our method directly learns the expected optimization function during training. To efficiently learn the function in a data-driven manner, we devise an attention-based model architecture inspired by the distribution-based parameterization of the expected objective. Our method is, to the best of our knowledge, the first to address all three bottlenecks within a single model. We evaluate DF2 on a synthetic problem, a wind power bidding problem, and a non-convex vaccine distribution problem, demonstrating the effectiveness of DF2.

MUBen: Benchmarking the Uncertainty of Pre-Trained Models for Molecular Property Prediction

Large Transformer models pre-trained on massive unlabeled molecular data have shown great success in predicting molecular properties. However, these models can be prone to overfitting during fine-tuning, resulting in over-confident predictions on test data that fall outside of the training distribution. To address this issue, uncertainty quantification (UQ) methods can be used to improve the models' calibration of predictions. Although many UQ approaches exist, not all of them lead to improved performance. While some studies have used UQ to improve molecular pre-trained models, the process of selecting suitable backbone and UQ methods for reliable molecular uncertainty estimation remains underexplored. To address this gap, we present MUBen, which evaluates different combinations of backbone and UQ models to quantify their performance for both property prediction and uncertainty estimation. By fine-tuning various backbone molecular representation models using different molecular descriptors as inputs with UQ methods from different categories, we critically assess the influence of architectural decisions and training strategies. Our study offers insights for selecting UQ and backbone models, which can facilitate research on uncertainty-critical applications in fields such as materials science and drug discovery.