Impact of Bias on School Admissions and Targeted Interventions

There is an inherent problem in the way students are evaluated - be it standardized testing, interviews or essays. These evaluation criteria cannot be adjusted to account for the impact of implicit bias, socio-economic status or even opportunities available to the students. Motivated by this, we present, to the best of our knowledge, the first mathematical analysis of the impact of deficiencies in evaluation mechanisms on the rank of schools that students get matched to. In particular, we analyze a double continuous model of schools and students, where all the students have a unanimous ranking for all the schools, and schools observe the potential of students to accept the best students from the available applicant pool. To account for bias in evaluations, we consider the group model of bias (Kleinberg and Raghavan 2018) where the schools can only observe a discounted potential for a subset of the candidates, instead of their actual potential. We show that under a natural matching mechanism, the ranking of the matched schools of both unbiased group and biased group of students are affected, with some of the latter being heavily penalized even for relatively small bias. Further, we find that schools have little incentive to change their evaluation mechanism, if their goal is the maximize the total potential of accepted students. Armed with this basic model and inferences, we show that the students who are most in need of additional resources to achieve their true potential are average-performing students, as opposed to high performers, thus questioning existing scholarship/aide mechanisms focusing on top performers. We further show, using computational experiments, that the qualitative take-aways from our model remain the same even if some of the assumptions are relaxed and we move, e.g., from a continuous to a discrete model and allow the bias factor to vary for each student.

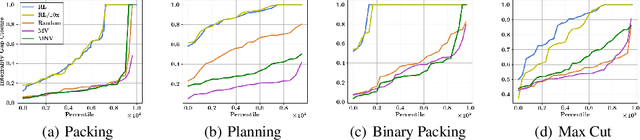
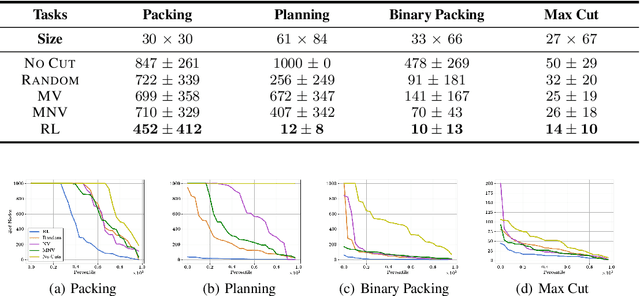
Reinforcement Learning for Integer Programming: Learning to Cut

Integer programming (IP) is a general optimization framework widely applicable to a variety of unstructured and structured problems arising in, e.g., scheduling, production planning, and graph optimization. As IP models many provably hard to solve problems, modern IP solvers rely on many heuristics. These heuristics are usually human-designed, and naturally prone to suboptimality. The goal of this work is to show that the performance of those solvers can be greatly enhanced using reinforcement learning (RL). In particular, we investigate a specific methodology for solving IPs, known as the Cutting Plane Method. This method is employed as a subroutine by all modern IP solvers. We present a deep RL formulation, network architecture, and algorithms for intelligent adaptive selection of cutting planes (aka cuts). Across a wide range of IP tasks, we show that the trained RL agent significantly outperforms human-designed heuristics, and effectively generalizes to 10X larger instances and across IP problem classes. The trained agent is also demonstrated to benefit the popular downstream application of cutting plane methods in Branch-and-Cut algorithm, which is the backbone of state-of-the-art commercial IP solvers.