Reinforcement Learning for Integer Programming: Learning to Cut
Paper and Code
Jun 11, 2019

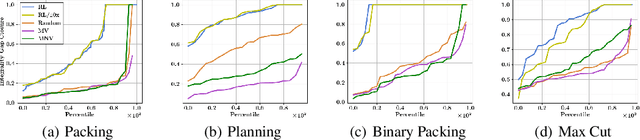
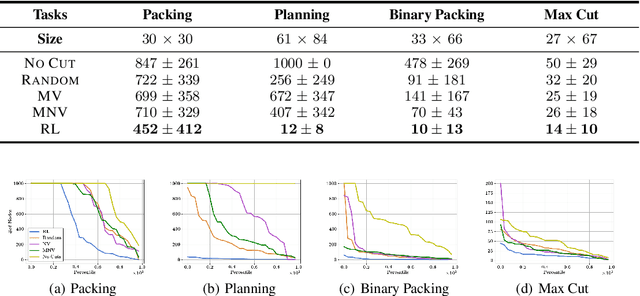
Integer programming (IP) is a general optimization framework widely applicable to a variety of unstructured and structured problems arising in, e.g., scheduling, production planning, and graph optimization. As IP models many provably hard to solve problems, modern IP solvers rely on many heuristics. These heuristics are usually human-designed, and naturally prone to suboptimality. The goal of this work is to show that the performance of those solvers can be greatly enhanced using reinforcement learning (RL). In particular, we investigate a specific methodology for solving IPs, known as the Cutting Plane Method. This method is employed as a subroutine by all modern IP solvers. We present a deep RL formulation, network architecture, and algorithms for intelligent adaptive selection of cutting planes (aka cuts). Across a wide range of IP tasks, we show that the trained RL agent significantly outperforms human-designed heuristics, and effectively generalizes to 10X larger instances and across IP problem classes. The trained agent is also demonstrated to benefit the popular downstream application of cutting plane methods in Branch-and-Cut algorithm, which is the backbone of state-of-the-art commercial IP solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge