The Randomized Elliptical Potential Lemma with an Application to Linear Thompson Sampling

In this note, we introduce a randomized version of the well-known elliptical potential lemma that is widely used in the analysis of algorithms in sequential learning and decision-making problems such as stochastic linear bandits. Our randomized elliptical potential lemma relaxes the Gaussian assumption on the observation noise and on the prior distribution of the problem parameters. We then use this generalization to prove an improved Bayesian regret bound for Thompson sampling for the linear stochastic bandits with changing action sets where prior and noise distributions are general. This bound is minimax optimal up to constants.

On Worst-case Regret of Linear Thompson Sampling

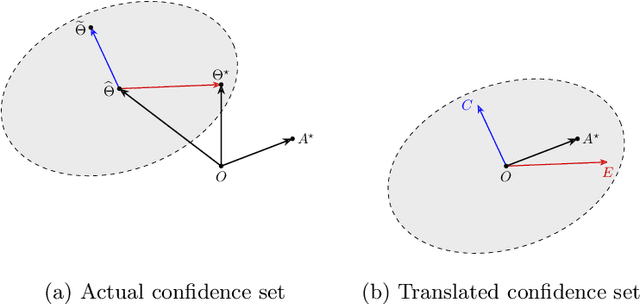
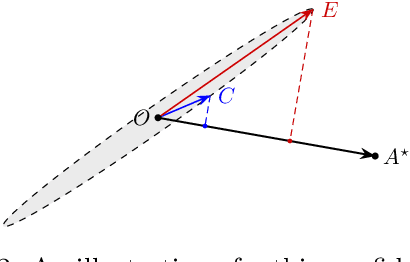
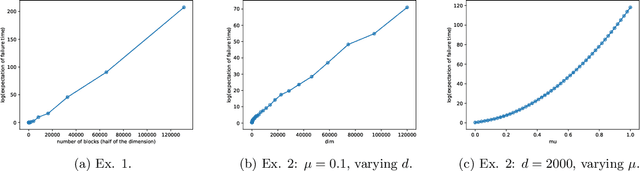
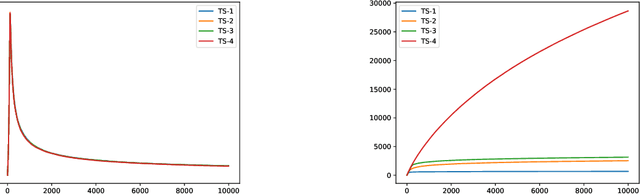
In this paper, we consider the worst-case regret of Linear Thompson Sampling (LinTS) for the linear bandit problem. Russo and Van Roy (2014) show that the Bayesian regret of LinTS is bounded above by $\widetilde{\mathcal{O}}(d\sqrt{T})$ where $T$ is the time horizon and $d$ is the number of parameters. While this bound matches the minimax lower-bounds for this problem up to logarithmic factors, the existence of a similar worst-case regret bound is still unknown. The only known worst-case regret bound for LinTS, due to Agrawal and Goyal (2013b); Abeille et al. (2017), is $\widetilde{\mathcal{O}}(d\sqrt{dT})$ which requires the posterior variance to be inflated by a factor of $\widetilde{\mathcal{O}}(\sqrt{d})$. While this bound is far from the minimax optimal rate by a factor of $\sqrt{d}$, in this paper we show that it is the best possible one can get, settling an open problem stated in Russo et al. (2018). Specifically, we construct examples to show that, without the inflation, LinTS can incur linear regret up to time $\exp(\mathcal{O}(d))$. We then demonstrate that, under mild conditions, a slightly modified version of LinTS requires only an $\widetilde{\mathcal{O}}(1)$ inflation where the constant depends on the diversity of the optimal arm.

Optimal and Greedy Algorithms for Multi-Armed Bandits with Many Arms

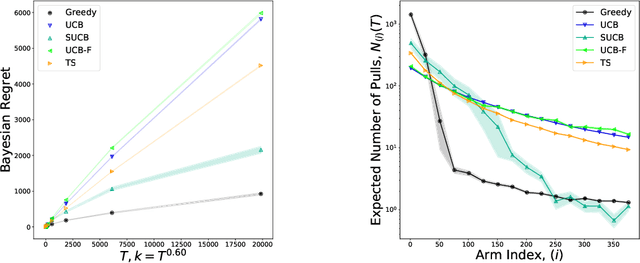
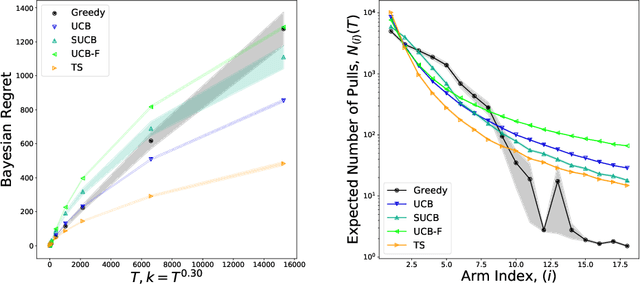
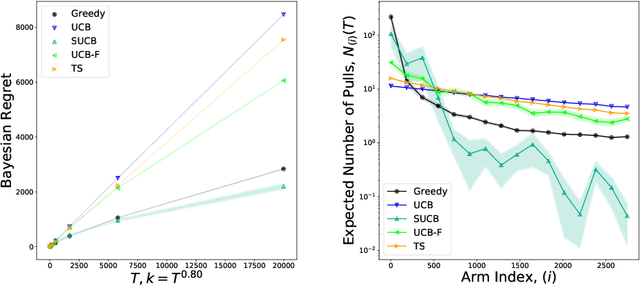
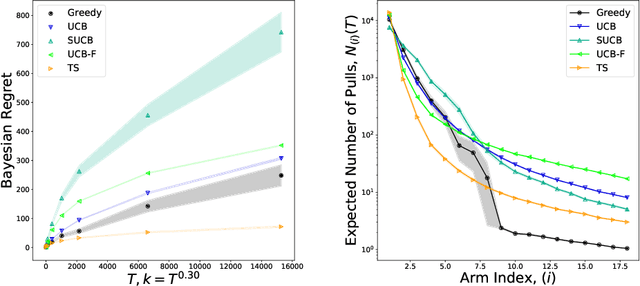
We characterize Bayesian regret in a stochastic multi-armed bandit problem with a large but finite number of arms. In particular, we assume the number of arms $k$ is $T^{\alpha}$, where $T$ is the time-horizon and $\alpha$ is in $(0,1)$. We consider a Bayesian setting where the reward distribution of each arm is drawn independently from a common prior, and provide a complete analysis of expected regret with respect to this prior. Our results exhibit a sharp distinction around $\alpha = 1/2$. When $\alpha < 1/2$, the fundamental lower bound on regret is $\Omega(k)$; and it is achieved by a standard UCB algorithm. When $\alpha > 1/2$, the fundamental lower bound on regret is $\Omega(\sqrt{T})$, and it is achieved by an algorithm that first subsamples $\sqrt{T}$ arms uniformly at random, then runs UCB on just this subset. Interestingly, we also find that a sufficiently large number of arms allows the decision-maker to benefit from "free" exploration if she simply uses a greedy algorithm. In particular, this greedy algorithm exhibits a regret of $\tilde{O}(\max(k,T/\sqrt{k}))$, which translates to a {\em sublinear} (though not optimal) regret in the time horizon. We show empirically that this is because the greedy algorithm rapidly disposes of underperforming arms, a beneficial trait in the many-armed regime. Technically, our analysis of the greedy algorithm involves a novel application of the Lundberg inequality, an upper bound for the ruin probability of a random walk; this approach may be of independent interest.

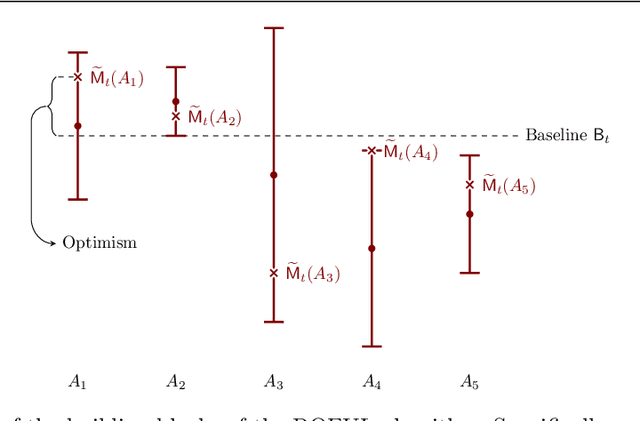
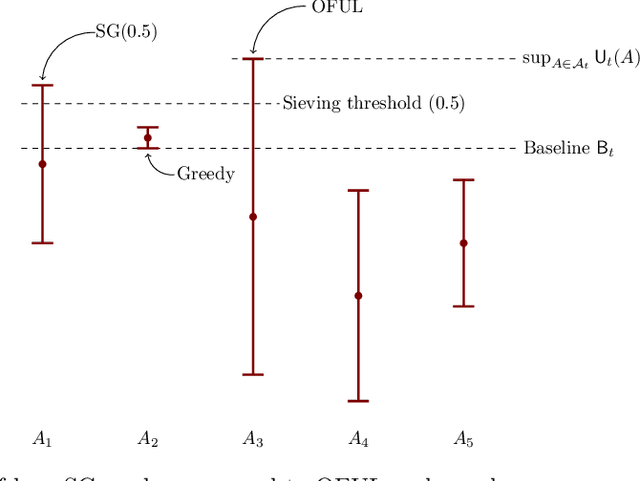
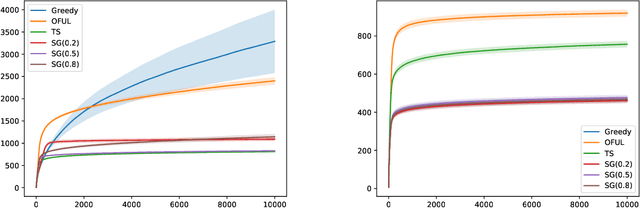
A General Framework to Analyze Stochastic Linear Bandit

In this paper we study the well-known stochastic linear bandit problem where a decision-maker sequentially chooses among a set of given actions in R^d, observes their noisy reward, and aims to maximize her cumulative expected reward over a horizon of length T. We introduce a general family of algorithms for the problem and prove that they are rate optimal. We also show that several well-known algorithms for the problem such as optimism in the face of uncertainty linear bandit (OFUL) and Thompson sampling (TS) are special cases of our family of algorithms. Therefore, we obtain a unified proof of rate optimality for both of these algorithms. Our results include both adversarial action sets (when actions are potentially selected by an adversary) and stochastic action sets (when actions are independently drawn from an unknown distribution). In terms of regret, our results apply to both Bayesian and worst-case regret settings. Our new unified analysis technique also yields a number of new results and solves two open problems known in the literature. Most notably, (1) we show that TS can incur a linear worst-case regret, unless it uses inflated (by a factor of $\sqrt{d}$) posterior variances at each step. This shows that the best known worst-case regret bound for TS, that is given by (Agrawal & Goyal, 2013; Abeille et al., 2017) and is worse (by a factor of \sqrt(d)) than the best known Bayesian regret bound given by Russo and Van Roy (2014) for TS, is tight. This settles an open problem stated in Russo et al., 2018. (2) Our proof also shows that TS can incur a linear Bayesian regret if it does not use the correct prior or noise distribution. (3) Under a generalized gap assumption and a margin condition, as in Goldenshluger & Zeevi, 2013, we obtain a poly-logarithmic (in $T$) regret bound for OFUL and TS in the stochastic setting.

Multi-scale Embedded CNN for Music Tagging

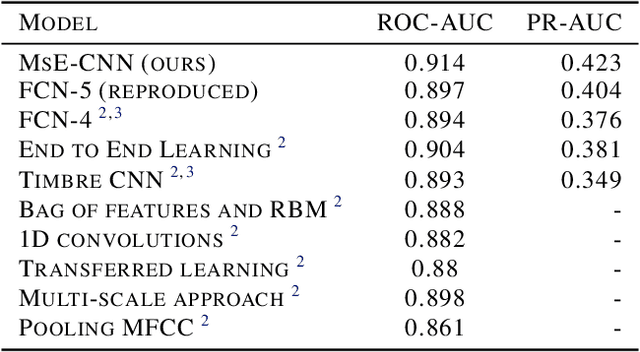
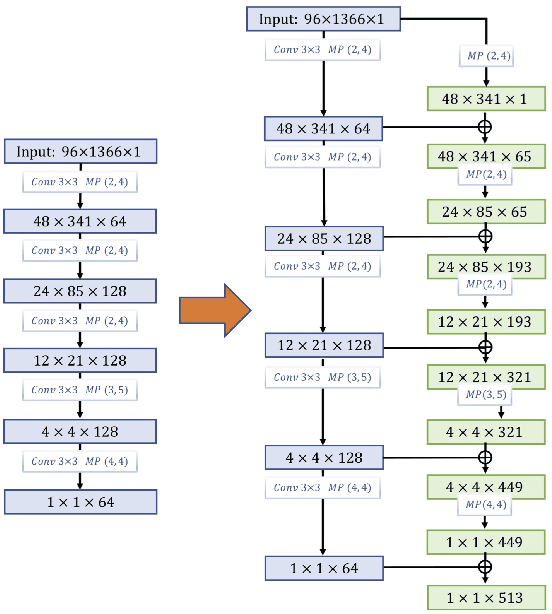
Convolutional neural networks (CNN) recently gained notable attraction in a variety of machine learning tasks: including music classification and style tagging. In this work, we propose implementing intermediate connections to the CNN architecture to facilitate the transfer of multi-scale/level knowledge between different layers. Our novel model for music tagging shows significant improvement in comparison to the proposed approaches in the literature, due to its ability to carry low-level timbral features to the last layer.

On Low-rank Trace Regression under General Sampling Distribution

A growing number of modern statistical learning problems involve estimating a large number of parameters from a (smaller) number of observations. In a subset of these problems (matrix completion, matrix compressed sensing, and multi-task learning) the unknown parameters form a high-dimensional matrix, and two popular approaches for the estimation are trace-norm regularized linear regression or alternating minimization. It is also known that these estimators satisfy certain optimal tail bounds under assumptions on rank, coherence, or spikiness of the unknown matrix. We study a general family of estimators and sampling distribution that include the above two estimators, and introduce a general notion of spikiness and rank for the unknown matrix. Next, we extend the existing literature on the analysis of these estimators and provide a unifying technique to prove tail bounds for the estimation error. We demonstrate the benefit of this generalization by studying its application to four problems of (1) matrix completion, (2) multi-task learning, (3) compressed sensing with Gaussian ensembles, and (4) compressed sensing with factored measurements. For (1) and (3), we recover matching tail bounds as those found in the literature, and for (2) and (4) we obtain (to the best of our knowledge) the first tail bounds. Our approach relies on a generic recipe to prove restricted strong convexity for the sampling operator of the trace regression, that only requires finding upper bounds on certain norms of the parameter matrix.