Optimal and Greedy Algorithms for Multi-Armed Bandits with Many Arms
Paper and Code
Feb 24, 2020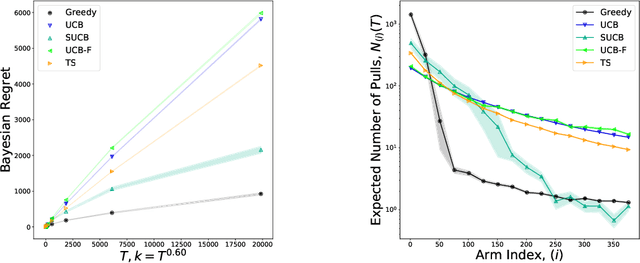
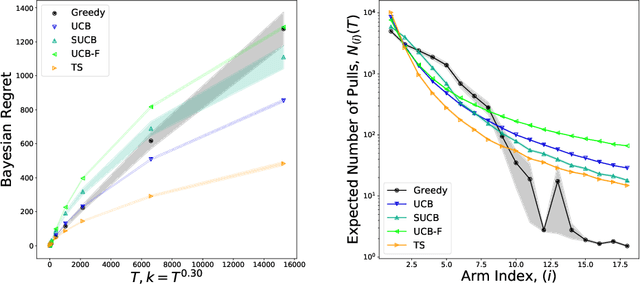
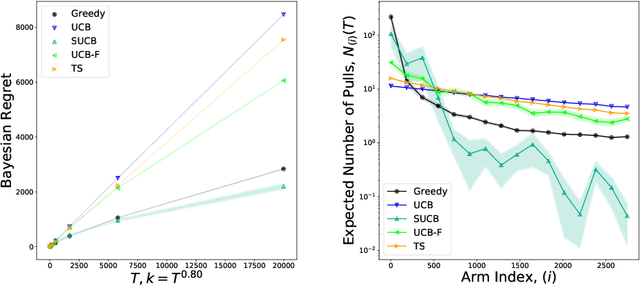
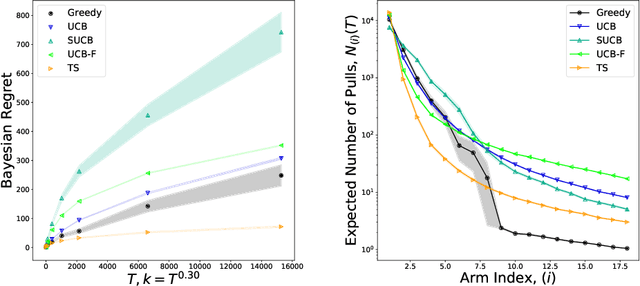
We characterize Bayesian regret in a stochastic multi-armed bandit problem with a large but finite number of arms. In particular, we assume the number of arms $k$ is $T^{\alpha}$, where $T$ is the time-horizon and $\alpha$ is in $(0,1)$. We consider a Bayesian setting where the reward distribution of each arm is drawn independently from a common prior, and provide a complete analysis of expected regret with respect to this prior. Our results exhibit a sharp distinction around $\alpha = 1/2$. When $\alpha < 1/2$, the fundamental lower bound on regret is $\Omega(k)$; and it is achieved by a standard UCB algorithm. When $\alpha > 1/2$, the fundamental lower bound on regret is $\Omega(\sqrt{T})$, and it is achieved by an algorithm that first subsamples $\sqrt{T}$ arms uniformly at random, then runs UCB on just this subset. Interestingly, we also find that a sufficiently large number of arms allows the decision-maker to benefit from "free" exploration if she simply uses a greedy algorithm. In particular, this greedy algorithm exhibits a regret of $\tilde{O}(\max(k,T/\sqrt{k}))$, which translates to a {\em sublinear} (though not optimal) regret in the time horizon. We show empirically that this is because the greedy algorithm rapidly disposes of underperforming arms, a beneficial trait in the many-armed regime. Technically, our analysis of the greedy algorithm involves a novel application of the Lundberg inequality, an upper bound for the ruin probability of a random walk; this approach may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge