A General Framework to Analyze Stochastic Linear Bandit

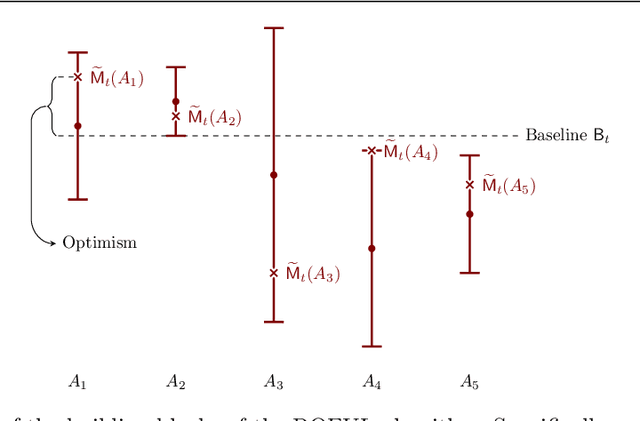
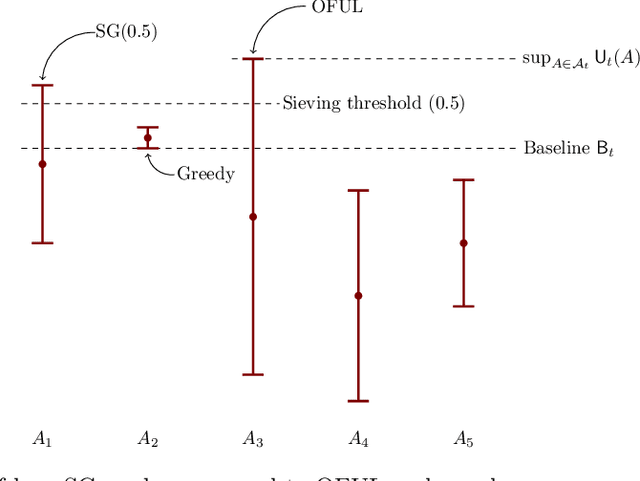
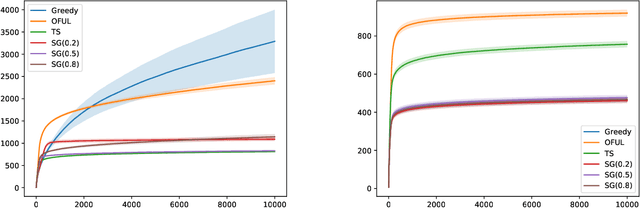
In this paper we study the well-known stochastic linear bandit problem where a decision-maker sequentially chooses among a set of given actions in R^d, observes their noisy reward, and aims to maximize her cumulative expected reward over a horizon of length T. We introduce a general family of algorithms for the problem and prove that they are rate optimal. We also show that several well-known algorithms for the problem such as optimism in the face of uncertainty linear bandit (OFUL) and Thompson sampling (TS) are special cases of our family of algorithms. Therefore, we obtain a unified proof of rate optimality for both of these algorithms. Our results include both adversarial action sets (when actions are potentially selected by an adversary) and stochastic action sets (when actions are independently drawn from an unknown distribution). In terms of regret, our results apply to both Bayesian and worst-case regret settings. Our new unified analysis technique also yields a number of new results and solves two open problems known in the literature. Most notably, (1) we show that TS can incur a linear worst-case regret, unless it uses inflated (by a factor of $\sqrt{d}$) posterior variances at each step. This shows that the best known worst-case regret bound for TS, that is given by (Agrawal & Goyal, 2013; Abeille et al., 2017) and is worse (by a factor of \sqrt(d)) than the best known Bayesian regret bound given by Russo and Van Roy (2014) for TS, is tight. This settles an open problem stated in Russo et al., 2018. (2) Our proof also shows that TS can incur a linear Bayesian regret if it does not use the correct prior or noise distribution. (3) Under a generalized gap assumption and a margin condition, as in Goldenshluger & Zeevi, 2013, we obtain a poly-logarithmic (in $T$) regret bound for OFUL and TS in the stochastic setting.