Semi-parametric dynamic contextual pricing

We consider a canonical revenue maximization problem where customers arrive sequentially; each customer is interested in buying one product, and the customer purchases the product if her valuation for it exceeds the price set by the seller. The valuations of customers are not observed by the seller; however, the seller can leverage contextual information available to her in the form of noisy covariate vectors describing the customer's history and the product's type to set prices. The seller can learn the relationship between covariates and customer valuations by experimenting with prices and observing transaction outcomes. We consider a semi-parametric model where the relationship between the expectation of the log of valuation and the covariates is linear (hence parametric) and the residual uncertainty distribution, i.e., the noise distribution, is non-parametric. We develop a pricing policy, DEEP-C, which learns this relationship with minimal exploration and in turn achieves optimal regret asymptotically in the time horizon.

Bandit Learning with Positive Externalities

In many platforms, user arrivals exhibit a self-reinforcing behavior: future user arrivals are likely to have preferences similar to users who were satisfied in the past. In other words, arrivals exhibit positive externalities. We study multiarmed bandit (MAB) problems with positive externalities. We show that the self-reinforcing preferences may lead standard benchmark algorithms such as UCB to exhibit linear regret. We develop a new algorithm, Balanced Exploration (BE), which explores arms carefully to avoid suboptimal convergence of arrivals before sufficient evidence is gathered. We also introduce an adaptive variant of BE which successively eliminates suboptimal arms. We analyze their asymptotic regret, and establish optimality by showing that no algorithm can perform better.

Adaptive Matching for Expert Systems with Uncertain Task Types

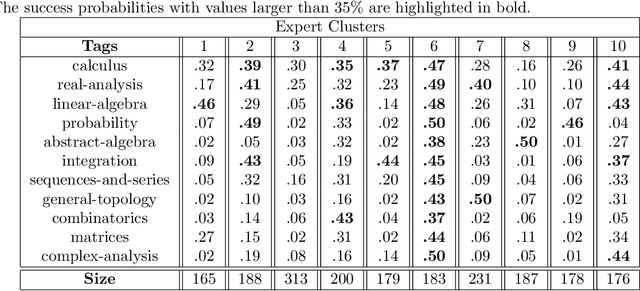
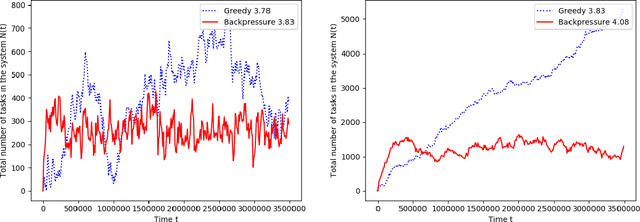
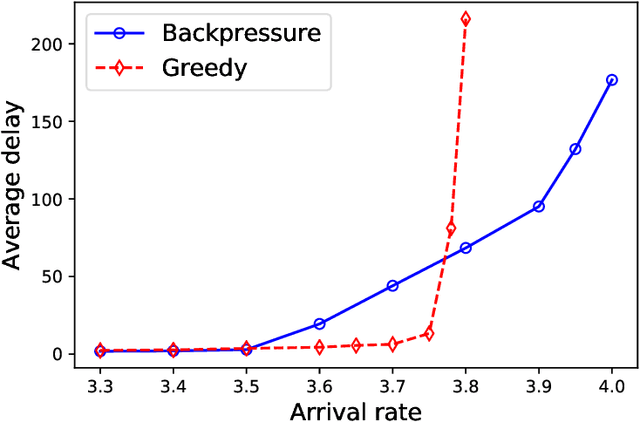
A matching in a two-sided market often incurs an externality: a matched resource may become unavailable to the other side of the market, at least for a while. This is especially an issue in online platforms involving human experts as the expert resources are often scarce. The efficient utilization of experts in these platforms is made challenging by the fact that the information available about the parties involved is usually limited. To address this challenge, we develop a model of a task-expert matching system where a task is matched to an expert using not only the prior information about the task but also the feedback obtained from the past matches. In our model the tasks arrive online while the experts are fixed and constrained by a finite service capacity. For this model, we characterize the maximum task resolution throughput a platform can achieve. We show that the natural greedy approaches where each expert is assigned a task most suitable to her skill is suboptimal, as it does not internalize the above externality. We develop a throughput optimal backpressure algorithm which does so by accounting for the `congestion' among different task types. Finally, we validate our model and confirm our theoretical findings with data-driven simulations via logs of Math.StackExchange, a StackOverflow forum dedicated to mathematics.

Optimal Testing in the Experiment-rich Regime

Motivated by the widespread adoption of large-scale A/B testing in industry, we propose a new experimentation framework for the setting where potential experiments are abundant (i.e., many hypotheses are available to test), and observations are costly; we refer to this as the experiment-rich regime. Such scenarios require the experimenter to internalize the opportunity cost of assigning a sample to a particular experiment. We fully characterize the optimal policy and give an algorithm to compute it. Furthermore, we develop a simple heuristic that also provides intuition for the optimal policy. We use simulations based on real data to compare both the optimal algorithm and the heuristic to other natural alternative experimental design frameworks. In particular, we discuss the paradox of power: high-powered classical tests can lead to highly inefficient sampling in the experiment-rich regime.