Adaptive Matching for Expert Systems with Uncertain Task Types

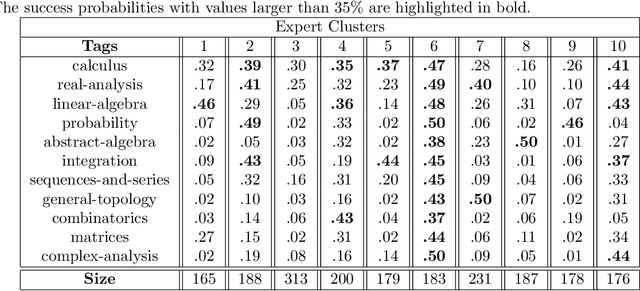
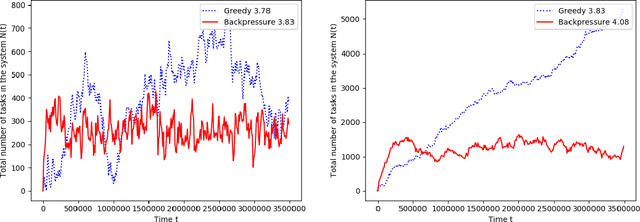
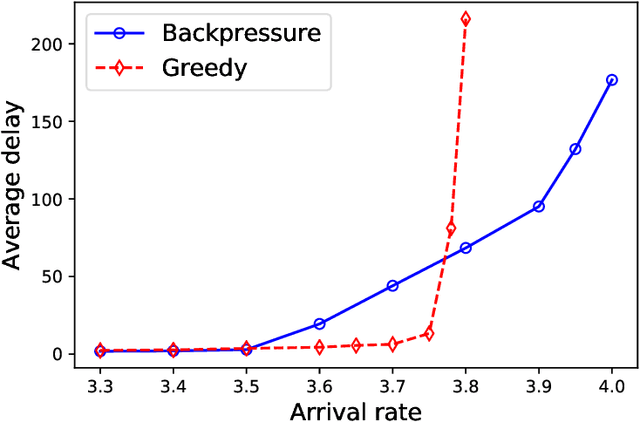
A matching in a two-sided market often incurs an externality: a matched resource may become unavailable to the other side of the market, at least for a while. This is especially an issue in online platforms involving human experts as the expert resources are often scarce. The efficient utilization of experts in these platforms is made challenging by the fact that the information available about the parties involved is usually limited. To address this challenge, we develop a model of a task-expert matching system where a task is matched to an expert using not only the prior information about the task but also the feedback obtained from the past matches. In our model the tasks arrive online while the experts are fixed and constrained by a finite service capacity. For this model, we characterize the maximum task resolution throughput a platform can achieve. We show that the natural greedy approaches where each expert is assigned a task most suitable to her skill is suboptimal, as it does not internalize the above externality. We develop a throughput optimal backpressure algorithm which does so by accounting for the `congestion' among different task types. Finally, we validate our model and confirm our theoretical findings with data-driven simulations via logs of Math.StackExchange, a StackOverflow forum dedicated to mathematics.

Non-Backtracking Spectrum of Degree-Corrected Stochastic Block Models

Motivated by community detection, we characterise the spectrum of the non-backtracking matrix $B$ in the Degree-Corrected Stochastic Block Model. Specifically, we consider a random graph on $n$ vertices partitioned into two equal-sized clusters. The vertices have i.i.d. weights $\{ \phi_u \}_{u=1}^n$ with second moment $\Phi^{(2)}$. The intra-cluster connection probability for vertices $u$ and $v$ is $\frac{\phi_u \phi_v}{n}a$ and the inter-cluster connection probability is $\frac{\phi_u \phi_v}{n}b$. We show that with high probability, the following holds: The leading eigenvalue of the non-backtracking matrix $B$ is asymptotic to $\rho = \frac{a+b}{2} \Phi^{(2)}$. The second eigenvalue is asymptotic to $\mu_2 = \frac{a-b}{2} \Phi^{(2)}$ when $\mu_2^2 > \rho$, but asymptotically bounded by $\sqrt{\rho}$ when $\mu_2^2 \leq \rho$. All the remaining eigenvalues are asymptotically bounded by $\sqrt{\rho}$. As a result, a clustering positively-correlated with the true communities can be obtained based on the second eigenvector of $B$ in the regime where $\mu_2^2 > \rho.$ In a previous work we obtained that detection is impossible when $\mu_2^2 < \rho,$ meaning that there occurs a phase-transition in the sparse regime of the Degree-Corrected Stochastic Block Model. As a corollary, we obtain that Degree-Corrected Erd\H{o}s-R\'enyi graphs asymptotically satisfy the graph Riemann hypothesis, a quasi-Ramanujan property. A by-product of our proof is a weak law of large numbers for local-functionals on Degree-Corrected Stochastic Block Models, which could be of independent interest.

A spectral method for community detection in moderately-sparse degree-corrected stochastic block models

We consider community detection in Degree-Corrected Stochastic Block Models (DC-SBM). We propose a spectral clustering algorithm based on a suitably normalized adjacency matrix. We show that this algorithm consistently recovers the block-membership of all but a vanishing fraction of nodes, in the regime where the lowest degree is of order log$(n)$ or higher. Recovery succeeds even for very heterogeneous degree-distributions. The used algorithm does not rely on parameters as input. In particular, it does not need to know the number of communities.

An Impossibility Result for Reconstruction in a Degree-Corrected Planted-Partition Model

We consider a Degree-Corrected Planted-Partition model: a random graph on $n$ nodes with two asymptotically equal-sized clusters. The model parameters are two constants $a,b > 0$ and an i.i.d. sequence of weights $(\phi_u)_{u=1}^n$, with finite second moment $\Phi^{(2)}$. Vertices $u$ and $v$ are joined by an edge with probability $\frac{\phi_u \phi_v}{n}a$ when they are in the same class and with probability $\frac{\phi_u \phi_v}{n}b$ otherwise. We prove that it is information-theoretically impossible to estimate the spins in a way positively correlated with the true community structure when $(a-b)^2 \Phi^{(2)} \leq 2(a+b)$. A by-product of our proof is a precise coupling-result for local-neighbourhoods in Degree-Corrected Planted-Partition models, which could be of independent interest.