Beyond Noise: Privacy-Preserving Decentralized Learning with Virtual Nodes

Decentralized learning (DL) enables collaborative learning without a server and without training data leaving the users' devices. However, the models shared in DL can still be used to infer training data. Conventional privacy defenses such as differential privacy and secure aggregation fall short in effectively safeguarding user privacy in DL. We introduce Shatter, a novel DL approach in which nodes create virtual nodes (VNs) to disseminate chunks of their full model on their behalf. This enhances privacy by (i) preventing attackers from collecting full models from other nodes, and (ii) hiding the identity of the original node that produced a given model chunk. We theoretically prove the convergence of Shatter and provide a formal analysis demonstrating how Shatter reduces the efficacy of attacks compared to when exchanging full models between participating nodes. We evaluate the convergence and attack resilience of Shatter with existing DL algorithms, with heterogeneous datasets, and against three standard privacy attacks, including gradient inversion. Our evaluation shows that Shatter not only renders these privacy attacks infeasible when each node operates 16 VNs but also exhibits a positive impact on model convergence compared to standard DL. This enhanced privacy comes with a manageable increase in communication volume.

Decentralized Optimization with Heterogeneous Delays: a Continuous-Time Approach

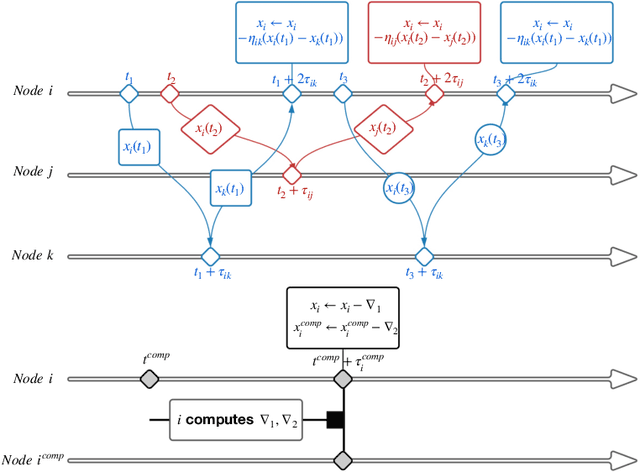
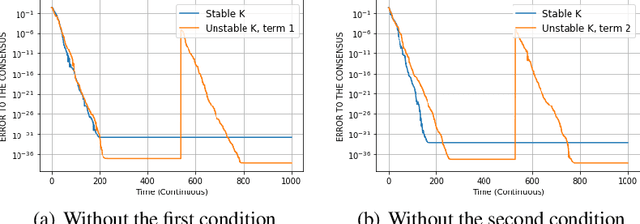
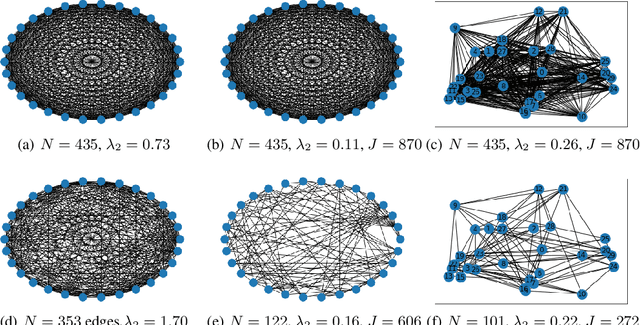
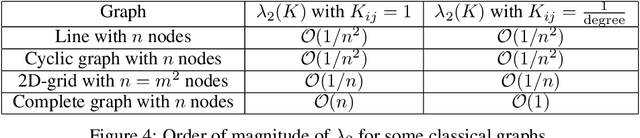
In decentralized optimization, nodes of a communication network privately possess a local objective function, and communicate using gossip-based methods in order to minimize the average of these per-node objectives. While synchronous algorithms can be heavily slowed down by a few nodes and edges in the graph (the straggler problem), their asynchronous counterparts lack from a sharp analysis taking into account heterogeneous delays in the communication network. In this paper, we propose a novel continuous-time framework to analyze asynchronous algorithms, which does not require to define a global ordering of the events, and allows to finely characterize the time complexity in the presence of (heterogeneous) delays. Using this framework, we describe a fully asynchronous decentralized algorithm to minimize the sum of smooth and strongly convex functions. Our algorithm (DCDM, Delayed Coordinate Dual Method), based on delayed randomized gossip communications and local computational updates, achieves an asynchronous speed-up: the rate of convergence is tightly characterized in terms of the eigengap of the graph weighted by local delays only, instead of the global worst-case delays as in previous analyses.

Adaptive Matching for Expert Systems with Uncertain Task Types

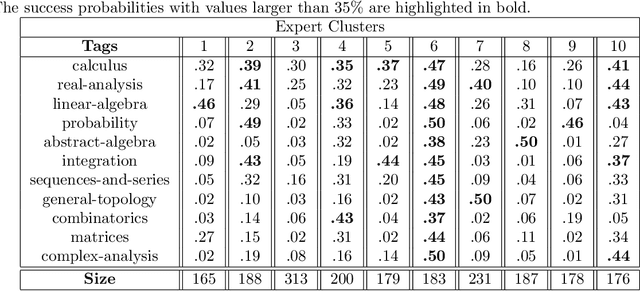
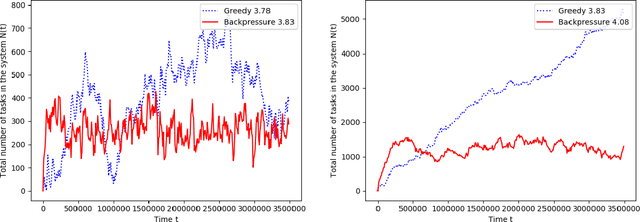
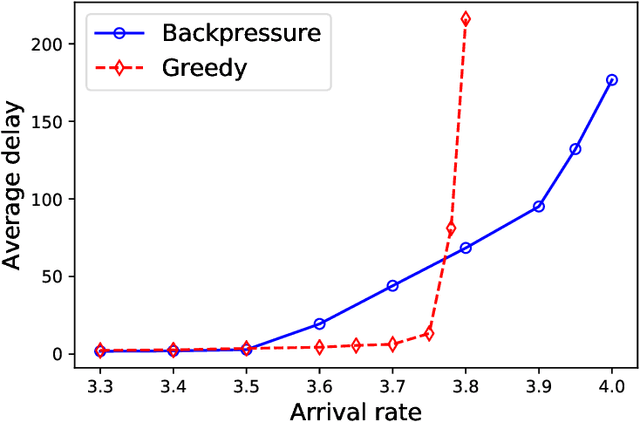
A matching in a two-sided market often incurs an externality: a matched resource may become unavailable to the other side of the market, at least for a while. This is especially an issue in online platforms involving human experts as the expert resources are often scarce. The efficient utilization of experts in these platforms is made challenging by the fact that the information available about the parties involved is usually limited. To address this challenge, we develop a model of a task-expert matching system where a task is matched to an expert using not only the prior information about the task but also the feedback obtained from the past matches. In our model the tasks arrive online while the experts are fixed and constrained by a finite service capacity. For this model, we characterize the maximum task resolution throughput a platform can achieve. We show that the natural greedy approaches where each expert is assigned a task most suitable to her skill is suboptimal, as it does not internalize the above externality. We develop a throughput optimal backpressure algorithm which does so by accounting for the `congestion' among different task types. Finally, we validate our model and confirm our theoretical findings with data-driven simulations via logs of Math.StackExchange, a StackOverflow forum dedicated to mathematics.

From Small-World Networks to Comparison-Based Search

The problem of content search through comparisons has recently received considerable attention. In short, a user searching for a target object navigates through a database in the following manner: the user is asked to select the object most similar to her target from a small list of objects. A new object list is then presented to the user based on her earlier selection. This process is repeated until the target is included in the list presented, at which point the search terminates. This problem is known to be strongly related to the small-world network design problem. However, contrary to prior work, which focuses on cases where objects in the database are equally popular, we consider here the case where the demand for objects may be heterogeneous. We show that, under heterogeneous demand, the small-world network design problem is NP-hard. Given the above negative result, we propose a novel mechanism for small-world design and provide an upper bound on its performance under heterogeneous demand. The above mechanism has a natural equivalent in the context of content search through comparisons, and we establish both an upper bound and a lower bound for the performance of this mechanism. These bounds are intuitively appealing, as they depend on the entropy of the demand as well as its doubling constant, a quantity capturing the topology of the set of target objects. They also illustrate interesting connections between comparison-based search to classic results from information theory. Finally, we propose an adaptive learning algorithm for content search that meets the performance guarantees achieved by the above mechanisms.