Decentralized Optimization with Heterogeneous Delays: a Continuous-Time Approach
Paper and Code
Jun 07, 2021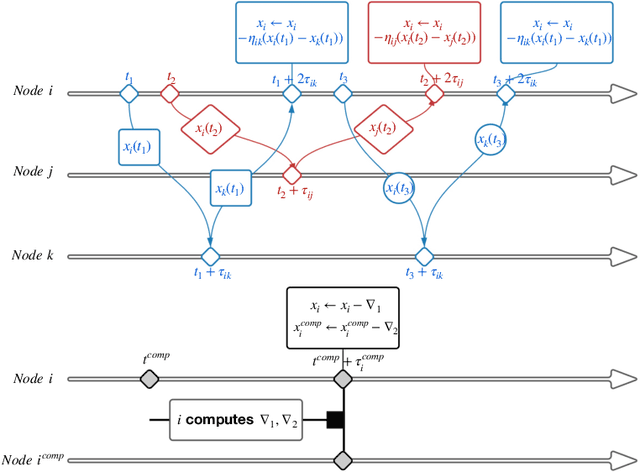
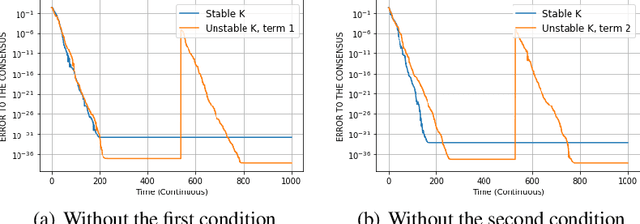
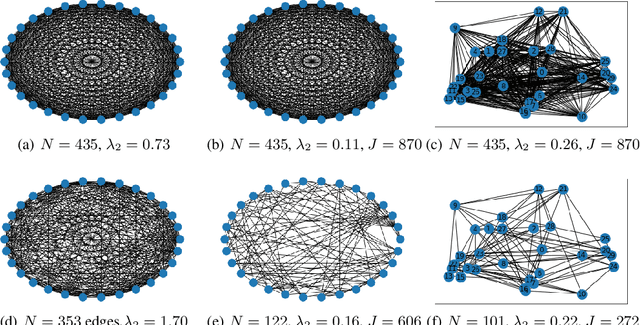
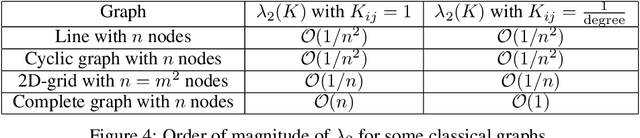
In decentralized optimization, nodes of a communication network privately possess a local objective function, and communicate using gossip-based methods in order to minimize the average of these per-node objectives. While synchronous algorithms can be heavily slowed down by a few nodes and edges in the graph (the straggler problem), their asynchronous counterparts lack from a sharp analysis taking into account heterogeneous delays in the communication network. In this paper, we propose a novel continuous-time framework to analyze asynchronous algorithms, which does not require to define a global ordering of the events, and allows to finely characterize the time complexity in the presence of (heterogeneous) delays. Using this framework, we describe a fully asynchronous decentralized algorithm to minimize the sum of smooth and strongly convex functions. Our algorithm (DCDM, Delayed Coordinate Dual Method), based on delayed randomized gossip communications and local computational updates, achieves an asynchronous speed-up: the rate of convergence is tightly characterized in terms of the eigengap of the graph weighted by local delays only, instead of the global worst-case delays as in previous analyses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge