CGKN: A Deep Learning Framework for Modeling Complex Dynamical Systems and Efficient Data Assimilation

Deep learning is widely used to predict complex dynamical systems in many scientific and engineering areas. However, the black-box nature of these deep learning models presents significant challenges for carrying out simultaneous data assimilation (DA), which is a crucial technique for state estimation, model identification, and reconstructing missing data. Integrating ensemble-based DA methods with nonlinear deep learning models is computationally expensive and may suffer from large sampling errors. To address these challenges, we introduce a deep learning framework designed to simultaneously provide accurate forecasts and efficient DA. It is named Conditional Gaussian Koopman Network (CGKN), which transforms general nonlinear systems into nonlinear neural differential equations with conditional Gaussian structures. CGKN aims to retain essential nonlinear components while applying systematic and minimal simplifications to facilitate the development of analytic formulae for nonlinear DA. This allows for seamless integration of DA performance into the deep learning training process, eliminating the need for empirical tuning as required in ensemble methods. CGKN compensates for structural simplifications by lifting the dimension of the system, which is motivated by Koopman theory. Nevertheless, CGKN exploits special nonlinear dynamics within the lifted space. This enables the model to capture extreme events and strong non-Gaussian features in joint and marginal distributions with appropriate uncertainty quantification. We demonstrate the effectiveness of CGKN for both prediction and DA on three strongly nonlinear and non-Gaussian turbulent systems: the projected stochastic Burgers--Sivashinsky equation, the Lorenz 96 system, and the El Ni\~no-Southern Oscillation. The results justify the robustness and computational efficiency of CGKN.

SimBench: A Rule-Based Multi-Turn Interaction Benchmark for Evaluating an LLM's Ability to Generate Digital Twins

We introduce SimBench, a benchmark designed to evaluate the proficiency of student large language models (S-LLMs) in generating digital twins (DTs) that can be used in simulators for virtual testing. Given a collection of S-LLMs, this benchmark enables the ranking of the S-LLMs based on their ability to produce high-quality DTs. We demonstrate this by comparing over 20 open- and closed-source S-LLMs. Using multi-turn interactions, SimBench employs a rule-based judge LLM (J-LLM) that leverages both predefined rules and human-in-the-loop guidance to assign scores for the DTs generated by the S-LLM, thus providing a consistent and expert-inspired evaluation protocol. The J-LLM is specific to a simulator, and herein the proposed benchmarking approach is demonstrated in conjunction with the Chrono multi-physics simulator. Chrono provided the backdrop used to assess an S-LLM in relation to the latter's ability to create digital twins for multibody dynamics, finite element analysis, vehicle dynamics, robotic dynamics, and sensor simulations. The proposed benchmarking principle is broadly applicable and enables the assessment of an S-LLM's ability to generate digital twins for other simulation packages. All code and data are available at https://github.com/uwsbel/SimBench.

Data-Driven Stochastic Closure Modeling via Conditional Diffusion Model and Neural Operator

Closure models are widely used in simulating complex multiscale dynamical systems such as turbulence and the earth system, for which direct numerical simulation that resolves all scales is often too expensive. For those systems without a clear scale separation, deterministic and local closure models often lack enough generalization capability, which limits their performance in many real-world applications. In this work, we propose a data-driven modeling framework for constructing stochastic and non-local closure models via conditional diffusion model and neural operator. Specifically, the Fourier neural operator is incorporated into a score-based diffusion model, which serves as a data-driven stochastic closure model for complex dynamical systems governed by partial differential equations (PDEs). We also demonstrate how accelerated sampling methods can improve the efficiency of the data-driven stochastic closure model. The results show that the proposed methodology provides a systematic approach via generative machine learning techniques to construct data-driven stochastic closure models for multiscale dynamical systems with continuous spatiotemporal fields.

CGNSDE: Conditional Gaussian Neural Stochastic Differential Equation for Modeling Complex Systems and Data Assimilation

A new knowledge-based and machine learning hybrid modeling approach, called conditional Gaussian neural stochastic differential equation (CGNSDE), is developed to facilitate modeling complex dynamical systems and implementing analytic formulae of the associated data assimilation (DA). In contrast to the standard neural network predictive models, the CGNSDE is designed to effectively tackle both forward prediction tasks and inverse state estimation problems. The CGNSDE starts by exploiting a systematic causal inference via information theory to build a simple knowledge-based nonlinear model that nevertheless captures as much explainable physics as possible. Then, neural networks are supplemented to the knowledge-based model in a specific way, which not only characterizes the remaining features that are challenging to model with simple forms but also advances the use of analytic formulae to efficiently compute the nonlinear DA solution. These analytic formulae are used as an additional computationally affordable loss to train the neural networks that directly improve the DA accuracy. This DA loss function promotes the CGNSDE to capture the interactions between state variables and thus advances its modeling skills. With the DA loss, the CGNSDE is more capable of estimating extreme events and quantifying the associated uncertainty. Furthermore, crucial physical properties in many complex systems, such as the translate-invariant local dependence of state variables, can significantly simplify the neural network structures and facilitate the CGNSDE to be applied to high-dimensional systems. Numerical experiments based on chaotic systems with intermittency and strong non-Gaussian features indicate that the CGNSDE outperforms knowledge-based regression models, and the DA loss further enhances the modeling skills of the CGNSDE.

Learning About Structural Errors in Models of Complex Dynamical Systems

Complex dynamical systems are notoriously difficult to model because some degrees of freedom (e.g., small scales) may be computationally unresolvable or are incompletely understood, yet they are dynamically important. For example, the small scales of cloud dynamics and droplet formation are crucial for controlling climate, yet are unresolvable in global climate models. Semi-empirical closure models for the effects of unresolved degrees of freedom often exist and encode important domain-specific knowledge. Building on such closure models and correcting them through learning the structural errors can be an effective way of fusing data with domain knowledge. Here we describe a general approach, principles, and algorithms for learning about structural errors. Key to our approach is to include structural error models inside the models of complex systems, for example, in closure models for unresolved scales. The structural errors then map, usually nonlinearly, to observable data. As a result, however, mismatches between model output and data are only indirectly informative about structural errors, due to a lack of labeled pairs of inputs and outputs of structural error models. Additionally, derivatives of the model may not exist or be readily available. We discuss how structural error models can be learned from indirect data with derivative-free Kalman inversion algorithms and variants, how sparsity constraints enforce a "do no harm" principle, and various ways of modeling structural errors. We also discuss the merits of using non-local and/or stochastic error models. In addition, we demonstrate how data assimilation techniques can assist the learning about structural errors in non-ergodic systems. The concepts and algorithms are illustrated in two numerical examples based on the Lorenz-96 system and a human glucose-insulin model.

Operator Learning for Continuous Spatial-Temporal Model with A Hybrid Optimization Scheme

Partial differential equations are often used in the spatial-temporal modeling of complex dynamical systems in many engineering applications. In this work, we build on the recent progress of operator learning and present a data-driven modeling framework that is continuous in both space and time. A key feature of the proposed model is the resolution-invariance with respect to both spatial and temporal discretizations. To improve the long-term performance of the calibrated model, we further propose a hybrid optimization scheme that leverages both gradient-based and derivative-free optimization methods and efficiently trains on both short-term time series and long-term statistics. We investigate the performance of the spatial-temporal continuous learning framework with three numerical examples, including the viscous Burgers' equation, the Navier-Stokes equations, and the Kuramoto-Sivashinsky equation. The results confirm the resolution-invariance of the proposed modeling framework and also demonstrate stable long-term simulations with only short-term time series data. In addition, we show that the proposed model can better predict long-term statistics via the hybrid optimization scheme with a combined use of short-term and long-term data.

CEBoosting: Online Sparse Identification of Dynamical Systems with Regime Switching by Causation Entropy Boosting

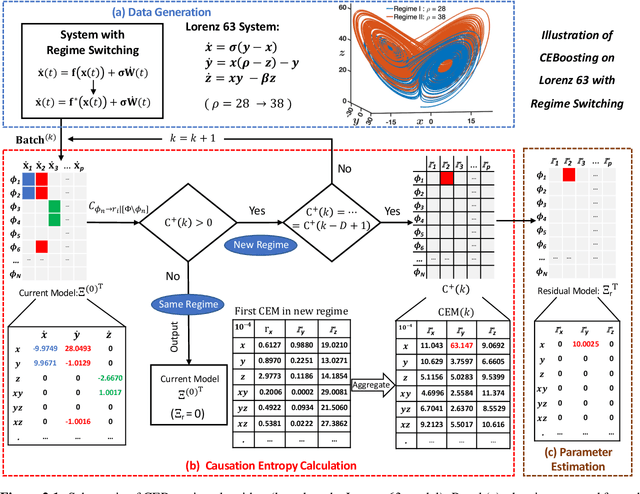
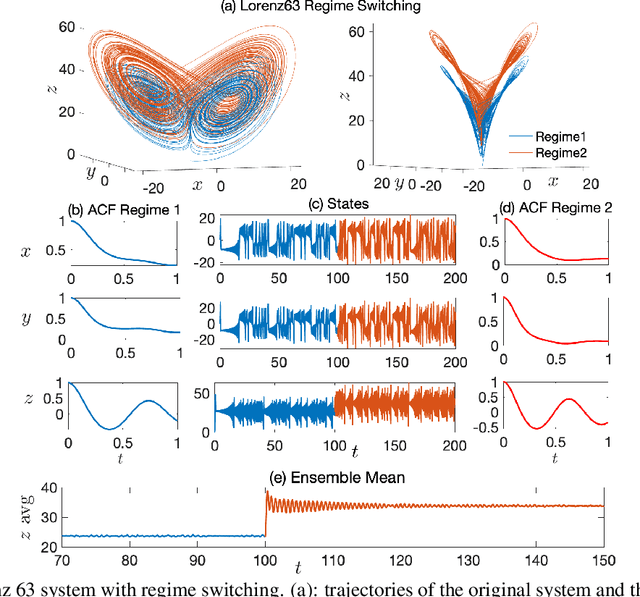
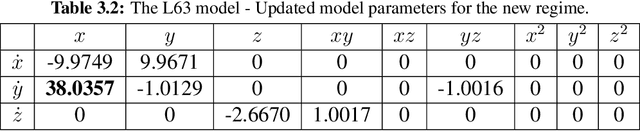
Regime switching is ubiquitous in many complex dynamical systems with multiscale features, chaotic behavior, and extreme events. In this paper, a causation entropy boosting (CEBoosting) strategy is developed to facilitate the detection of regime switching and the discovery of the dynamics associated with the new regime via online model identification. The causation entropy, which can be efficiently calculated, provides a logic value of each candidate function in a pre-determined library. The reversal of one or a few such causation entropy indicators associated with the model calibrated for the current regime implies the detection of regime switching. Despite the short length of each batch formed by the sequential data, the accumulated value of causation entropy corresponding to a sequence of data batches leads to a robust indicator. With the detected rectification of the model structure, the subsequent parameter estimation becomes a quadratic optimization problem, which is solved using closed analytic formulae. Using the Lorenz 96 model, it is shown that the causation entropy indicator can be efficiently calculated, and the method applies to moderately large dimensional systems. The CEBoosting algorithm is also adaptive to the situation with partial observations. It is shown via a stochastic parameterized model that the CEBoosting strategy can be combined with data assimilation to identify regime switching triggered by the unobserved latent processes. In addition, the CEBoosting method is applied to a nonlinear paradigm model for topographic mean flow interaction, demonstrating the online detection of regime switching in the presence of strong intermittency and extreme events.

Enforcing Deterministic Constraints on Generative Adversarial Networks for Emulating Physical Systems

Generative adversarial networks (GANs) are initially proposed to generate images by learning from a large number of samples. Recently, GANs have been used to emulate complex physical systems such as turbulent flows. However, a critical question must be answered before GANs can be considered trusted emulators for physical systems: do GANs-generated samples conform to the various physical constraints? These include both deterministic constraints (e.g., conservation laws) and statistical constraints (e.g., energy spectrum in turbulent flows). The latter has been studied in a companion paper (Wu et al. 2019. Enforcing statistical constraints in generative adversarial networks for modeling chaotic dynamical systems. arxiv:1905.06841). In the present work, we enforce deterministic yet approximate constraints on GANs by incorporating them into the loss function of the generator. We evaluate the performance of physics-constrained GANs on two representative tasks with geometrical constraints (generating points on circles) and differential constraints (generating divergence-free flow velocity fields), respectively. In both cases, the constrained GANs produced samples that precisely conform to the underlying constraints, even though the constraints are only enforced approximately. More importantly, the imposed constraints significantly accelerate the convergence and improve the robustness in the training. These improvements are noteworthy, as the convergence and robustness are two well-known obstacles in the training of GANs.

Enforcing Statistical Constraints in Generative Adversarial Networks for Modeling Chaotic Dynamical Systems

Simulating complex physical systems often involves solving partial differential equations (PDEs) with some closures due to the presence of multi-scale physics that cannot be fully resolved. Therefore, reliable and accurate closure models for unresolved physics remains an important requirement for many computational physics problems, e.g., turbulence simulation. Recently, several researchers have adopted generative adversarial networks (GANs), a novel paradigm of training machine learning models, to generate solutions of PDEs-governed complex systems without having to numerically solve these PDEs. However, GANs are known to be difficult in training and likely to converge to local minima, where the generated samples do not capture the true statistics of the training data. In this work, we present a statistical constrained generative adversarial network by enforcing constraints of covariance from the training data, which results in an improved machine-learning-based emulator to capture the statistics of the training data generated by solving fully resolved PDEs. We show that such a statistical regularization leads to better performance compared to standard GANs, measured by (1) the constrained model's ability to more faithfully emulate certain physical properties of the system and (2) the significantly reduced (by up to 80%) training time to reach the solution. We exemplify this approach on the Rayleigh-Benard convection, a turbulent flow system that is an idealized model of the Earth's atmosphere. With the growth of high-fidelity simulation databases of physical systems, this work suggests great potential for being an alternative to the explicit modeling of closures or parameterizations for unresolved physics, which are known to be a major source of uncertainty in simulating multi-scale physical systems, e.g., turbulence or Earth's climate.