CGKN: A Deep Learning Framework for Modeling Complex Dynamical Systems and Efficient Data Assimilation

Deep learning is widely used to predict complex dynamical systems in many scientific and engineering areas. However, the black-box nature of these deep learning models presents significant challenges for carrying out simultaneous data assimilation (DA), which is a crucial technique for state estimation, model identification, and reconstructing missing data. Integrating ensemble-based DA methods with nonlinear deep learning models is computationally expensive and may suffer from large sampling errors. To address these challenges, we introduce a deep learning framework designed to simultaneously provide accurate forecasts and efficient DA. It is named Conditional Gaussian Koopman Network (CGKN), which transforms general nonlinear systems into nonlinear neural differential equations with conditional Gaussian structures. CGKN aims to retain essential nonlinear components while applying systematic and minimal simplifications to facilitate the development of analytic formulae for nonlinear DA. This allows for seamless integration of DA performance into the deep learning training process, eliminating the need for empirical tuning as required in ensemble methods. CGKN compensates for structural simplifications by lifting the dimension of the system, which is motivated by Koopman theory. Nevertheless, CGKN exploits special nonlinear dynamics within the lifted space. This enables the model to capture extreme events and strong non-Gaussian features in joint and marginal distributions with appropriate uncertainty quantification. We demonstrate the effectiveness of CGKN for both prediction and DA on three strongly nonlinear and non-Gaussian turbulent systems: the projected stochastic Burgers--Sivashinsky equation, the Lorenz 96 system, and the El Ni\~no-Southern Oscillation. The results justify the robustness and computational efficiency of CGKN.

Data-Driven Stochastic Closure Modeling via Conditional Diffusion Model and Neural Operator

Closure models are widely used in simulating complex multiscale dynamical systems such as turbulence and the earth system, for which direct numerical simulation that resolves all scales is often too expensive. For those systems without a clear scale separation, deterministic and local closure models often lack enough generalization capability, which limits their performance in many real-world applications. In this work, we propose a data-driven modeling framework for constructing stochastic and non-local closure models via conditional diffusion model and neural operator. Specifically, the Fourier neural operator is incorporated into a score-based diffusion model, which serves as a data-driven stochastic closure model for complex dynamical systems governed by partial differential equations (PDEs). We also demonstrate how accelerated sampling methods can improve the efficiency of the data-driven stochastic closure model. The results show that the proposed methodology provides a systematic approach via generative machine learning techniques to construct data-driven stochastic closure models for multiscale dynamical systems with continuous spatiotemporal fields.

CGNSDE: Conditional Gaussian Neural Stochastic Differential Equation for Modeling Complex Systems and Data Assimilation

A new knowledge-based and machine learning hybrid modeling approach, called conditional Gaussian neural stochastic differential equation (CGNSDE), is developed to facilitate modeling complex dynamical systems and implementing analytic formulae of the associated data assimilation (DA). In contrast to the standard neural network predictive models, the CGNSDE is designed to effectively tackle both forward prediction tasks and inverse state estimation problems. The CGNSDE starts by exploiting a systematic causal inference via information theory to build a simple knowledge-based nonlinear model that nevertheless captures as much explainable physics as possible. Then, neural networks are supplemented to the knowledge-based model in a specific way, which not only characterizes the remaining features that are challenging to model with simple forms but also advances the use of analytic formulae to efficiently compute the nonlinear DA solution. These analytic formulae are used as an additional computationally affordable loss to train the neural networks that directly improve the DA accuracy. This DA loss function promotes the CGNSDE to capture the interactions between state variables and thus advances its modeling skills. With the DA loss, the CGNSDE is more capable of estimating extreme events and quantifying the associated uncertainty. Furthermore, crucial physical properties in many complex systems, such as the translate-invariant local dependence of state variables, can significantly simplify the neural network structures and facilitate the CGNSDE to be applied to high-dimensional systems. Numerical experiments based on chaotic systems with intermittency and strong non-Gaussian features indicate that the CGNSDE outperforms knowledge-based regression models, and the DA loss further enhances the modeling skills of the CGNSDE.

Operator Learning for Continuous Spatial-Temporal Model with A Hybrid Optimization Scheme

Partial differential equations are often used in the spatial-temporal modeling of complex dynamical systems in many engineering applications. In this work, we build on the recent progress of operator learning and present a data-driven modeling framework that is continuous in both space and time. A key feature of the proposed model is the resolution-invariance with respect to both spatial and temporal discretizations. To improve the long-term performance of the calibrated model, we further propose a hybrid optimization scheme that leverages both gradient-based and derivative-free optimization methods and efficiently trains on both short-term time series and long-term statistics. We investigate the performance of the spatial-temporal continuous learning framework with three numerical examples, including the viscous Burgers' equation, the Navier-Stokes equations, and the Kuramoto-Sivashinsky equation. The results confirm the resolution-invariance of the proposed modeling framework and also demonstrate stable long-term simulations with only short-term time series data. In addition, we show that the proposed model can better predict long-term statistics via the hybrid optimization scheme with a combined use of short-term and long-term data.

CharacterChat: Learning towards Conversational AI with Personalized Social Support

In our modern, fast-paced, and interconnected world, the importance of mental well-being has grown into a matter of great urgency. However, traditional methods such as Emotional Support Conversations (ESC) face challenges in effectively addressing a diverse range of individual personalities. In response, we introduce the Social Support Conversation (S2Conv) framework. It comprises a series of support agents and the interpersonal matching mechanism, linking individuals with persona-compatible virtual supporters. Utilizing persona decomposition based on the MBTI (Myers-Briggs Type Indicator), we have created the MBTI-1024 Bank, a group that of virtual characters with distinct profiles. Through improved role-playing prompts with behavior preset and dynamic memory, we facilitate the development of the MBTI-S2Conv dataset, which contains conversations between the characters in the MBTI-1024 Bank. Building upon these foundations, we present CharacterChat, a comprehensive S2Conv system, which includes a conversational model driven by personas and memories, along with an interpersonal matching plugin model that dispatches the optimal supporters from the MBTI-1024 Bank for individuals with specific personas. Empirical results indicate the remarkable efficacy of CharacterChat in providing personalized social support and highlight the substantial advantages derived from interpersonal matching. The source code is available in \url{https://github.com/morecry/CharacterChat}.

CEBoosting: Online Sparse Identification of Dynamical Systems with Regime Switching by Causation Entropy Boosting

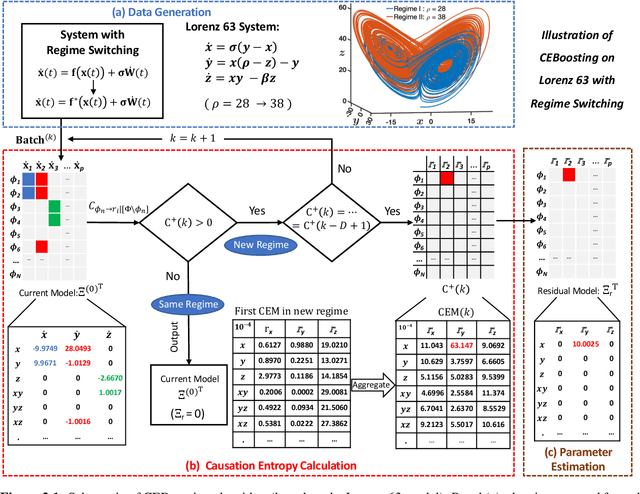
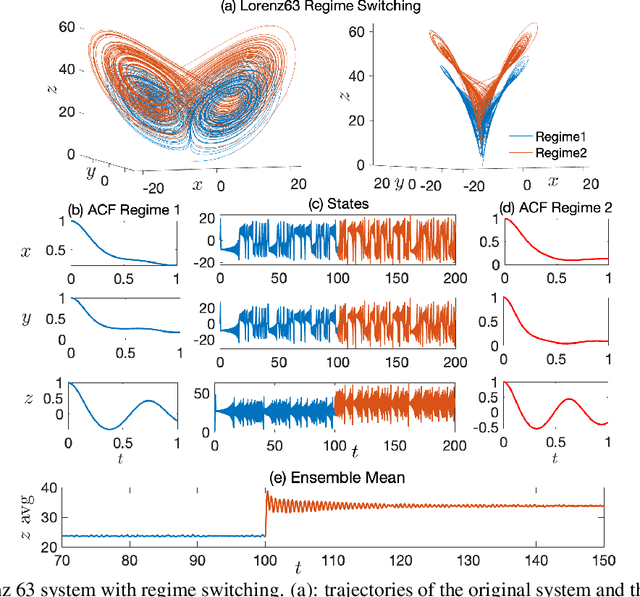
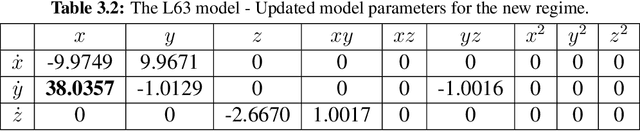
Regime switching is ubiquitous in many complex dynamical systems with multiscale features, chaotic behavior, and extreme events. In this paper, a causation entropy boosting (CEBoosting) strategy is developed to facilitate the detection of regime switching and the discovery of the dynamics associated with the new regime via online model identification. The causation entropy, which can be efficiently calculated, provides a logic value of each candidate function in a pre-determined library. The reversal of one or a few such causation entropy indicators associated with the model calibrated for the current regime implies the detection of regime switching. Despite the short length of each batch formed by the sequential data, the accumulated value of causation entropy corresponding to a sequence of data batches leads to a robust indicator. With the detected rectification of the model structure, the subsequent parameter estimation becomes a quadratic optimization problem, which is solved using closed analytic formulae. Using the Lorenz 96 model, it is shown that the causation entropy indicator can be efficiently calculated, and the method applies to moderately large dimensional systems. The CEBoosting algorithm is also adaptive to the situation with partial observations. It is shown via a stochastic parameterized model that the CEBoosting strategy can be combined with data assimilation to identify regime switching triggered by the unobserved latent processes. In addition, the CEBoosting method is applied to a nonlinear paradigm model for topographic mean flow interaction, demonstrating the online detection of regime switching in the presence of strong intermittency and extreme events.