Variational Shapley Network: A Probabilistic Approach to Self-Explaining Shapley values with Uncertainty Quantification

Shapley values have emerged as a foundational tool in machine learning (ML) for elucidating model decision-making processes. Despite their widespread adoption and unique ability to satisfy essential explainability axioms, computational challenges persist in their estimation when ($i$) evaluating a model over all possible subset of input feature combinations, ($ii$) estimating model marginals, and ($iii$) addressing variability in explanations. We introduce a novel, self-explaining method that simplifies the computation of Shapley values significantly, requiring only a single forward pass. Recognizing the deterministic treatment of Shapley values as a limitation, we explore incorporating a probabilistic framework to capture the inherent uncertainty in explanations. Unlike alternatives, our technique does not rely directly on the observed data space to estimate marginals; instead, it uses adaptable baseline values derived from a latent, feature-specific embedding space, generated by a novel masked neural network architecture. Evaluations on simulated and real datasets underscore our technique's robust predictive and explanatory performance.

A Coreset-based, Tempered Variational Posterior for Accurate and Scalable Stochastic Gaussian Process Inference

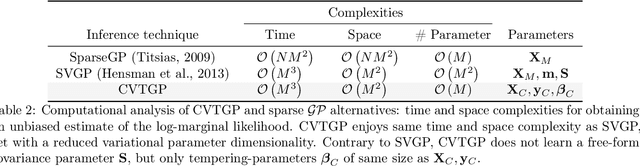
We present a novel stochastic variational Gaussian process ($\mathcal{GP}$) inference method, based on a posterior over a learnable set of weighted pseudo input-output points (coresets). Instead of a free-form variational family, the proposed coreset-based, variational tempered family for $\mathcal{GP}$s (CVTGP) is defined in terms of the $\mathcal{GP}$ prior and the data-likelihood; hence, accommodating the modeling inductive biases. We derive CVTGP's lower bound for the log-marginal likelihood via marginalization of the proposed posterior over latent $\mathcal{GP}$ coreset variables, and show it is amenable to stochastic optimization. CVTGP reduces the learnable parameter size to $\mathcal{O}(M)$, enjoys numerical stability, and maintains $\mathcal{O}(M^3)$ time- and $\mathcal{O}(M^2)$ space-complexity, by leveraging a coreset-based tempered posterior that, in turn, provides sparse and explainable representations of the data. Results on simulated and real-world regression problems with Gaussian observation noise validate that CVTGP provides better evidence lower-bound estimates and predictive root mean squared error than alternative stochastic $\mathcal{GP}$ inference methods.

Multi-armed bandits for online optimization of language model pre-training: the use case of dynamic masking

Transformer-based language models (TLMs) provide state-of-the-art performance in many modern natural language processing applications. TLM training is conducted in two phases. First, the model is pre-trained over large volumes of text to minimize a generic objective function, such as the Masked Language Model (MLM). Second, the model is fine-tuned in specific downstream tasks. Pre-training requires large volumes of data and high computational resources, while introducing many still unresolved design choices. For instance, selecting hyperparameters for language model pre-training is often carried out based on heuristics or grid-based searches. In this work, we propose a multi-armed bandit-based online optimization framework for the sequential selection of pre-training hyperparameters to optimize language model performance. We pose the pre-training procedure as a sequential decision-making task, where at each pre-training step, an agent must determine what hyperparameters to use towards optimizing the pre-training objective. We propose a Thompson sampling bandit algorithm, based on a surrogate Gaussian process reward model of the MLM pre-training objective, for its sequential minimization. We empirically show how the proposed Gaussian process based Thompson sampling pre-trains robust and well-performing language models. Namely, by sequentially selecting masking hyperparameters of the TLM, we achieve satisfactory performance in less epochs, not only in terms of the pre-training MLM objective, but in diverse downstream fine-tuning tasks. The proposed bandit-based technique provides an automated hyperparameter selection method for pre-training TLMs of interest to practitioners. In addition, our results indicate that, instead of MLM pre-training with fixed masking probabilities, sequentially adapting the masking hyperparameters improves both pre-training loss and downstream task metrics.

A generative, predictive model for menstrual cycle lengths that accounts for potential self-tracking artifacts in mobile health data

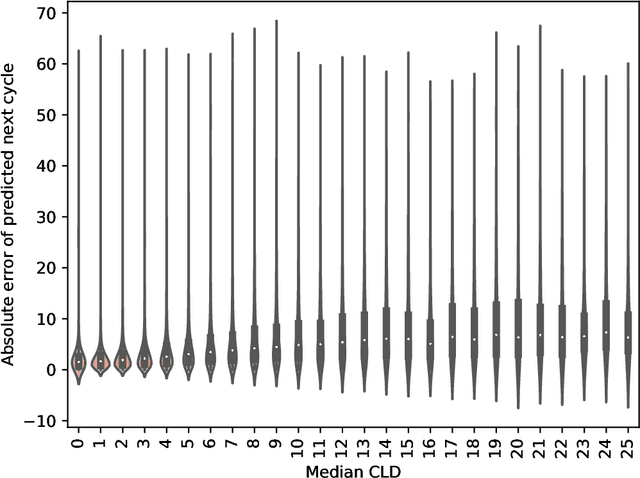
Mobile health (mHealth) apps such as menstrual trackers provide a rich source of self-tracked health observations that can be leveraged for health-relevant research. However, such data streams have questionable reliability since they hinge on user adherence to the app. Therefore, it is crucial for researchers to separate true behavior from self-tracking artifacts. By taking a machine learning approach to modeling self-tracked cycle lengths, we can both make more informed predictions and learn the underlying structure of the observed data. In this work, we propose and evaluate a hierarchical, generative model for predicting next cycle length based on previously-tracked cycle lengths that accounts explicitly for the possibility of users skipping tracking their period. Our model offers several advantages: 1) accounting explicitly for self-tracking artifacts yields better prediction accuracy as likelihood of skipping increases; 2) because it is a generative model, predictions can be updated online as a given cycle evolves, and we can gain interpretable insight into how these predictions change over time; and 3) its hierarchical nature enables modeling of an individual's cycle length history while incorporating population-level information. Our experiments using mHealth cycle length data encompassing over 186,000 menstruators with over 2 million natural menstrual cycles show that our method yields state-of-the-art performance against neural network-based and summary statistic-based baselines, while providing insights on disentangling menstrual patterns from self-tracking artifacts. This work can benefit users, mHealth app developers, and researchers in better understanding cycle patterns and user adherence.

Multi-Task Gaussian Processes and Dilated Convolutional Networks for Reconstruction of Reproductive Hormonal Dynamics

We present an end-to-end statistical framework for personalized, accurate, and minimally invasive modeling of female reproductive hormonal patterns. Reconstructing and forecasting the evolution of hormonal dynamics is a challenging task, but a critical one to improve general understanding of the menstrual cycle and personalized detection of potential health issues. Our goal is to infer and forecast individual hormone daily levels over time, while accommodating pragmatic and minimally invasive measurement settings. To that end, our approach combines the power of probabilistic generative models (i.e., multi-task Gaussian processes) with the flexibility of neural networks (i.e., a dilated convolutional architecture) to learn complex temporal mappings. To attain accurate hormone level reconstruction with as little data as possible, we propose a sampling mechanism for optimal reconstruction accuracy with limited sampling budget. Our results show the validity of our proposed hormonal dynamic modeling framework, as it provides accurate predictive performance across different realistic sampling budgets and outperforms baselines methods.

Phenotyping Endometriosis through Mixed Membership Models of Self-Tracking Data

We investigate the use of self-tracking data and unsupervised mixed-membership models to phenotype endometriosis. Endometriosis is a systemic, chronic condition of women in reproductive age and, at the same time, a highly enigmatic condition with no known biomarkers to monitor its progression and no established staging. We leverage data collected through a self-tracking app in an observational research study of over 2,800 women with endometriosis tracking their condition over a year and a half (456,900 observations overall). We extend a classical mixed-membership model to accommodate the idiosyncrasies of the data at hand (i.e., the multimodality of the tracked variables). Our experiments show that our approach identifies potential subtypes that are robust in terms of biases of self-tracked data (e.g., wide variations in tracking frequency amongst participants), as well as to variations in hyperparameters of the model. Jointly modeling a wide range of observations about participants (symptoms, quality of life, treatments) yields clinically meaningful subtypes that both validate what is already known about endometriosis and suggest new findings.

(Sequential) Importance Sampling Bandits

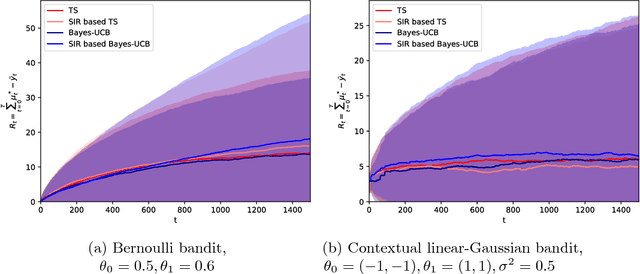
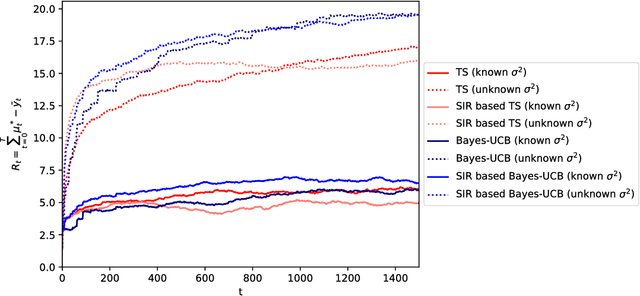
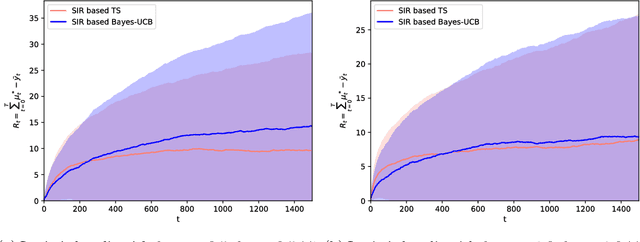
The multi-armed bandit (MAB) problem is a sequential allocation task where the goal is to learn a policy that maximizes long term payoff, where only the reward of the executed action is observed; i.e., sequential optimal decisions are made, while simultaneously learning how the world operates. In the stochastic setting, the reward for each action is generated from an unknown distribution. To decide the next optimal action to take, one must compute sufficient statistics of this unknown reward distribution, e.g. upper-confidence bounds (UCB), or expectations in Thompson sampling. Closed-form expressions for these statistics of interest are analytically intractable except for simple cases. We here propose to leverage Monte Carlo estimation and, in particular, the flexibility of (sequential) importance sampling (IS) to allow for accurate estimation of the statistics of interest within the MAB problem. IS methods estimate posterior densities or expectations in probabilistic models that are analytically intractable. We first show how IS can be combined with state-of-the-art MAB algorithms (Thompson sampling and Bayes-UCB) for classic (Bernoulli and contextual linear-Gaussian) bandit problems. Furthermore, we leverage the power of sequential IS to extend the applicability of these algorithms beyond the classic settings, and tackle additional useful cases. Specifically, we study the dynamic linear-Gaussian bandit, and both the static and dynamic logistic cases too. The flexibility of (sequential) importance sampling is shown to be fundamental for obtaining efficient estimates of the key sufficient statistics in these challenging scenarios.

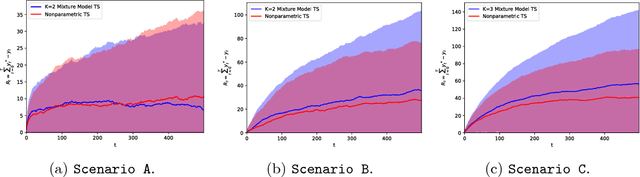
Nonparametric Gaussian mixture models for the multi-armed contextual bandit

The multi-armed bandit is a sequential allocation task where an agent must learn a policy that maximizes long term payoff, where only the reward of the played arm is observed at each iteration. In the stochastic setting, the reward for each action is generated from an unknown distribution, which depends on a given 'context', available at each interaction with the world. Thompson sampling is a generative, interpretable multi-armed bandit algorithm that has been shown both to perform well in practice, and to enjoy optimality properties for certain reward functions. Nevertheless, Thompson sampling requires sampling from parameter posteriors and calculation of expected rewards, which are possible for a very limited choice of distributions. We here extend Thompson sampling to more complex scenarios by adopting a very flexible set of reward distributions: nonparametric Gaussian mixture models. The generative process of Bayesian nonparametric mixtures naturally aligns with the Bayesian modeling of multi-armed bandits. This allows for the implementation of an efficient and flexible Thompson sampling algorithm: the nonparametric model autonomously determines its complexity in an online fashion, as it observes new rewards for the played arms. We show how the proposed method sequentially learns the nonparametric mixture model that best approximates the true underlying reward distribution. Our contribution is valuable for practical scenarios, as it avoids stringent model specifications, and yet attains reduced regret.

Bayesian bandits: balancing the exploration-exploitation tradeoff via double sampling

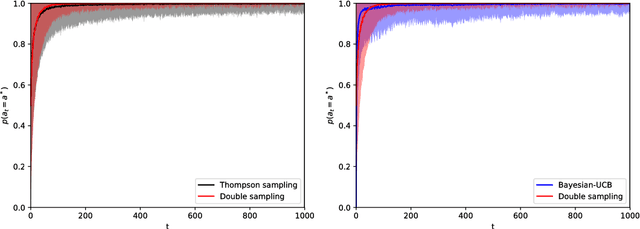
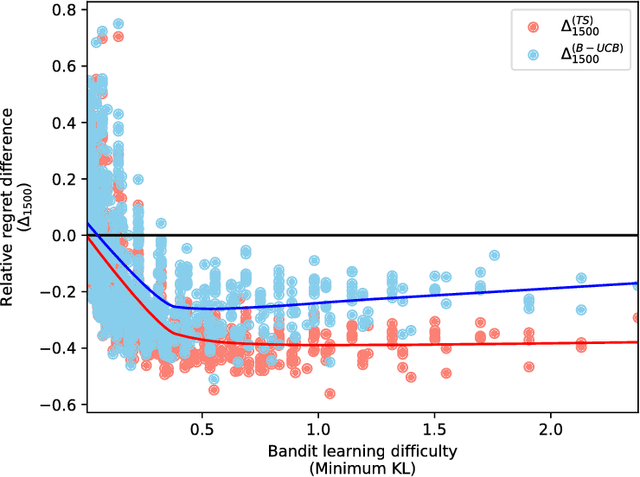
Reinforcement learning studies how to balance exploration and exploitation in real-world systems, optimizing interactions with the world while simultaneously learning how the world operates. One general class of algorithms for such learning is the multi-armed bandit setting. Randomized probability matching, based upon the Thompson sampling approach introduced in the 1930s, has recently been shown to perform well and to enjoy provable optimality properties. It permits generative, interpretable modeling in a Bayesian setting, where prior knowledge is incorporated, and the computed posteriors naturally capture the full state of knowledge. In this work, we harness the information contained in the Bayesian posterior and estimate its sufficient statistics via sampling. In several application domains, for example in health and medicine, each interaction with the world can be expensive and invasive, whereas drawing samples from the model is relatively inexpensive. Exploiting this viewpoint, we develop a double sampling technique driven by the uncertainty in the learning process: it favors exploitation when certain about the properties of each arm, exploring otherwise. The proposed algorithm does not make any distributional assumption and it is applicable to complex reward distributions, as long as Bayesian posterior updates are computable. Utilizing the estimated posterior sufficient statistics, double sampling autonomously balances the exploration-exploitation tradeoff to make better informed decisions. We empirically show its reduced cumulative regret when compared to state-of-the-art alternatives in representative bandit settings.

Variational inference for the multi-armed contextual bandit

In many biomedical, science, and engineering problems, one must sequentially decide which action to take next so as to maximize rewards. One general class of algorithms for optimizing interactions with the world, while simultaneously learning how the world operates, is the multi-armed bandit setting and, in particular, the contextual bandit case. In this setting, for each executed action, one observes rewards that are dependent on a given 'context', available at each interaction with the world. The Thompson sampling algorithm has recently been shown to enjoy provable optimality properties for this set of problems, and to perform well in real-world settings. It facilitates generative and interpretable modeling of the problem at hand. Nevertheless, the design and complexity of the model limit its application, since one must both sample from the distributions modeled and calculate their expected rewards. We here show how these limitations can be overcome using variational inference to approximate complex models, applying to the reinforcement learning case advances developed for the inference case in the machine learning community over the past two decades. We consider contextual multi-armed bandit applications where the true reward distribution is unknown and complex, which we approximate with a mixture model whose parameters are inferred via variational inference. We show how the proposed variational Thompson sampling approach is accurate in approximating the true distribution, and attains reduced regrets even with complex reward distributions. The proposed algorithm is valuable for practical scenarios where restrictive modeling assumptions are undesirable.