Variational Shapley Network: A Probabilistic Approach to Self-Explaining Shapley values with Uncertainty Quantification

Shapley values have emerged as a foundational tool in machine learning (ML) for elucidating model decision-making processes. Despite their widespread adoption and unique ability to satisfy essential explainability axioms, computational challenges persist in their estimation when ($i$) evaluating a model over all possible subset of input feature combinations, ($ii$) estimating model marginals, and ($iii$) addressing variability in explanations. We introduce a novel, self-explaining method that simplifies the computation of Shapley values significantly, requiring only a single forward pass. Recognizing the deterministic treatment of Shapley values as a limitation, we explore incorporating a probabilistic framework to capture the inherent uncertainty in explanations. Unlike alternatives, our technique does not rely directly on the observed data space to estimate marginals; instead, it uses adaptable baseline values derived from a latent, feature-specific embedding space, generated by a novel masked neural network architecture. Evaluations on simulated and real datasets underscore our technique's robust predictive and explanatory performance.

Maximum Likelihood Estimation of Flexible Survival Densities with Importance Sampling

Survival analysis is a widely-used technique for analyzing time-to-event data in the presence of censoring. In recent years, numerous survival analysis methods have emerged which scale to large datasets and relax traditional assumptions such as proportional hazards. These models, while being performant, are very sensitive to model hyperparameters including: (1) number of bins and bin size for discrete models and (2) number of cluster assignments for mixture-based models. Each of these choices requires extensive tuning by practitioners to achieve optimal performance. In addition, we demonstrate in empirical studies that: (1) optimal bin size may drastically differ based on the metric of interest (e.g., concordance vs brier score), and (2) mixture models may suffer from mode collapse and numerical instability. We propose a survival analysis approach which eliminates the need to tune hyperparameters such as mixture assignments and bin sizes, reducing the burden on practitioners. We show that the proposed approach matches or outperforms baselines on several real-world datasets.

A Coreset-based, Tempered Variational Posterior for Accurate and Scalable Stochastic Gaussian Process Inference

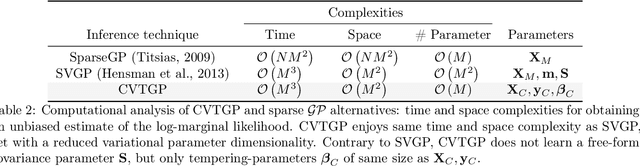
We present a novel stochastic variational Gaussian process ($\mathcal{GP}$) inference method, based on a posterior over a learnable set of weighted pseudo input-output points (coresets). Instead of a free-form variational family, the proposed coreset-based, variational tempered family for $\mathcal{GP}$s (CVTGP) is defined in terms of the $\mathcal{GP}$ prior and the data-likelihood; hence, accommodating the modeling inductive biases. We derive CVTGP's lower bound for the log-marginal likelihood via marginalization of the proposed posterior over latent $\mathcal{GP}$ coreset variables, and show it is amenable to stochastic optimization. CVTGP reduces the learnable parameter size to $\mathcal{O}(M)$, enjoys numerical stability, and maintains $\mathcal{O}(M^3)$ time- and $\mathcal{O}(M^2)$ space-complexity, by leveraging a coreset-based tempered posterior that, in turn, provides sparse and explainable representations of the data. Results on simulated and real-world regression problems with Gaussian observation noise validate that CVTGP provides better evidence lower-bound estimates and predictive root mean squared error than alternative stochastic $\mathcal{GP}$ inference methods.

What's in a Summary? Laying the Groundwork for Advances in Hospital-Course Summarization

Summarization of clinical narratives is a long-standing research problem. Here, we introduce the task of hospital-course summarization. Given the documentation authored throughout a patient's hospitalization, generate a paragraph that tells the story of the patient admission. We construct an English, text-to-text dataset of 109,000 hospitalizations (2M source notes) and their corresponding summary proxy: the clinician-authored "Brief Hospital Course" paragraph written as part of a discharge note. Exploratory analyses reveal that the BHC paragraphs are highly abstractive with some long extracted fragments; are concise yet comprehensive; differ in style and content organization from the source notes; exhibit minimal lexical cohesion; and represent silver-standard references. Our analysis identifies multiple implications for modeling this complex, multi-document summarization task.

Zero-Shot Clinical Acronym Expansion with a Hierarchical Metadata-Based Latent Variable Model

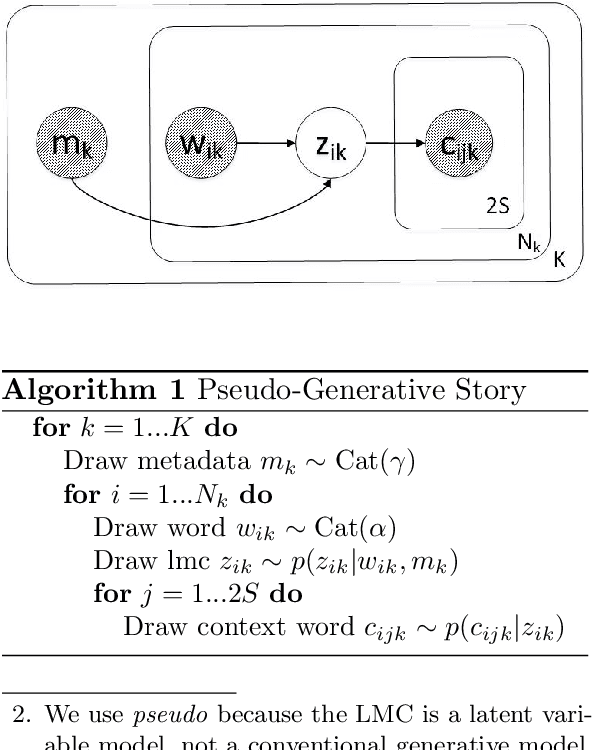
We introduce Latent Meaning Cells, a deep latent variable model which learns contextualized representations of words by combining local lexical context and metadata. Metadata can refer to granular context, such as section type, or to more global context, such as unique document ids. Reliance on metadata for contextualized representation learning is apropos in the clinical domain where text is semi-structured and expresses high variation in topics. We evaluate the LMC model on the task of clinical acronym expansion across three datasets. The LMC significantly outperforms a diverse set of baselines at a fraction of the pre-training cost and learns clinically coherent representations.