Bayesian bandits: balancing the exploration-exploitation tradeoff via double sampling
Paper and Code
Aug 08, 2018
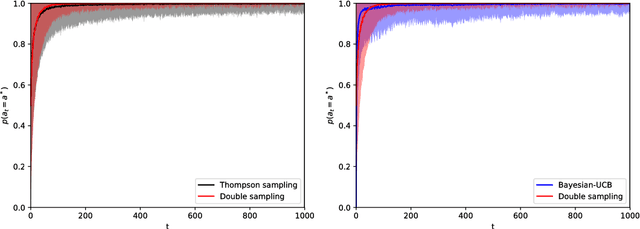

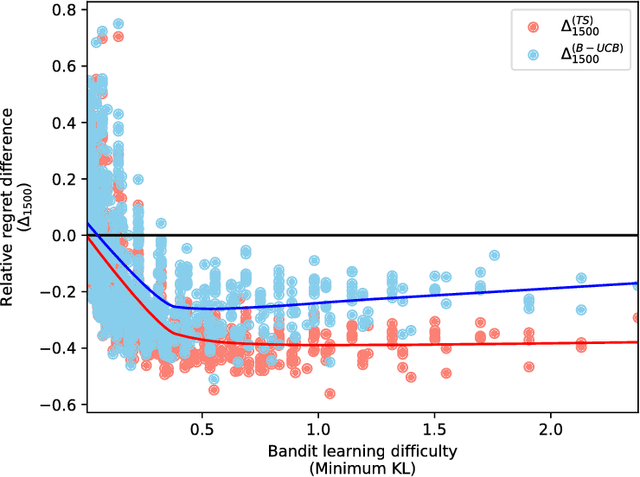
Reinforcement learning studies how to balance exploration and exploitation in real-world systems, optimizing interactions with the world while simultaneously learning how the world operates. One general class of algorithms for such learning is the multi-armed bandit setting. Randomized probability matching, based upon the Thompson sampling approach introduced in the 1930s, has recently been shown to perform well and to enjoy provable optimality properties. It permits generative, interpretable modeling in a Bayesian setting, where prior knowledge is incorporated, and the computed posteriors naturally capture the full state of knowledge. In this work, we harness the information contained in the Bayesian posterior and estimate its sufficient statistics via sampling. In several application domains, for example in health and medicine, each interaction with the world can be expensive and invasive, whereas drawing samples from the model is relatively inexpensive. Exploiting this viewpoint, we develop a double sampling technique driven by the uncertainty in the learning process: it favors exploitation when certain about the properties of each arm, exploring otherwise. The proposed algorithm does not make any distributional assumption and it is applicable to complex reward distributions, as long as Bayesian posterior updates are computable. Utilizing the estimated posterior sufficient statistics, double sampling autonomously balances the exploration-exploitation tradeoff to make better informed decisions. We empirically show its reduced cumulative regret when compared to state-of-the-art alternatives in representative bandit settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge