Optimal Low-Depth Quantum Signal-Processing Phase Estimation

Quantum effects like entanglement and coherent amplification can be used to drastically enhance the accuracy of quantum parameter estimation beyond classical limits. However, challenges such as decoherence and time-dependent errors hinder Heisenberg-limited amplification. We introduce Quantum Signal-Processing Phase Estimation algorithms that are robust against these challenges and achieve optimal performance as dictated by the Cram\'{e}r-Rao bound. These algorithms use quantum signal transformation to decouple interdependent phase parameters into largely orthogonal ones, ensuring that time-dependent errors in one do not compromise the accuracy of learning the other. Combining provably optimal classical estimation with near-optimal quantum circuit design, our approach achieves an unprecedented standard deviation accuracy of $10^{-4}$ radians for estimating unwanted swap angles in superconducting two-qubit experiments, using low-depth ($<10$) circuits. This represents up to two orders of magnitude improvement over existing methods. Theoretically and numerically, we demonstrate the optimality of our algorithm against time-dependent phase errors, observing that the variance of the time-sensitive parameter $\varphi$ scales faster than the asymptotic Heisenberg scaling in the small-depth regime. Our results are rigorously validated against the quantum Fisher information, confirming our protocol's ability to achieve unmatched precision for two-qubit gate learning.

Measuring Fairness in Large-Scale Recommendation Systems with Missing Labels

In large-scale recommendation systems, the vast array of items makes it infeasible to obtain accurate user preferences for each product, resulting in a common issue of missing labels. Typically, only items previously recommended to users have associated ground truth data. Although there is extensive research on fairness concerning fully observed user-item interactions, the challenge of fairness in scenarios with missing labels remains underexplored. Previous methods often treat these samples missing labels as negative, which can significantly deviate from the ground truth fairness metrics. Our study addresses this gap by proposing a novel method employing a small randomized traffic to estimate fairness metrics accurately. We present theoretical bounds for the estimation error of our fairness metric and support our findings with empirical evidence on real data. Our numerical experiments on synthetic and TikTok's real-world data validate our theory and show the efficiency and effectiveness of our novel methods. To the best of our knowledge, we are the first to emphasize the necessity of random traffic in dataset collection for recommendation fairness, the first to publish a fairness-related dataset from TikTok and to provide reliable estimates of fairness metrics in the context of large-scale recommendation systems with missing labels.

Beyond Heisenberg Limit Quantum Metrology through Quantum Signal Processing

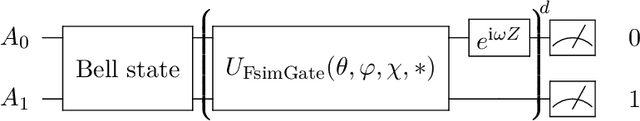
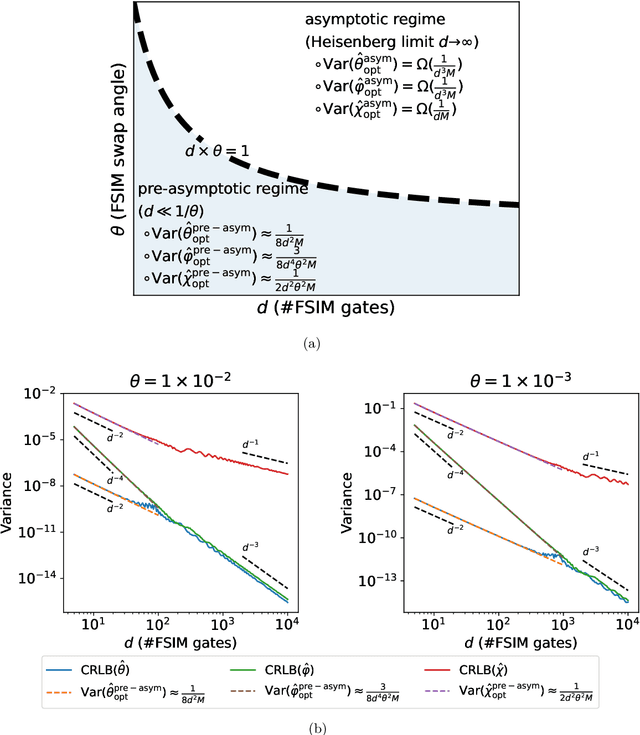
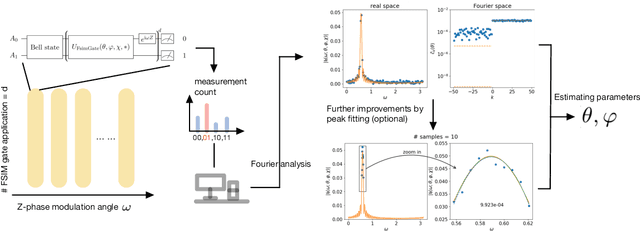
Leveraging quantum effects in metrology such as entanglement and coherence allows one to measure parameters with enhanced sensitivity. However, time-dependent noise can disrupt such Heisenberg-limited amplification. We propose a quantum-metrology method based on the quantum-signal-processing framework to overcome these realistic noise-induced limitations in practical quantum metrology. Our algorithm separates the gate parameter $\varphi$~(single-qubit Z phase) that is susceptible to time-dependent error from the target gate parameter $\theta$~(swap-angle between |10> and |01> states) that is largely free of time-dependent error. Our method achieves an accuracy of $10^{-4}$ radians in standard deviation for learning $\theta$ in superconducting-qubit experiments, outperforming existing alternative schemes by two orders of magnitude. We also demonstrate the increased robustness in learning time-dependent gate parameters through fast Fourier transformation and sequential phase difference. We show both theoretically and numerically that there is an interesting transition of the optimal metrology variance scaling as a function of circuit depth $d$ from the pre-asymptotic regime $d \ll 1/\theta$ to Heisenberg limit $d \to \infty$. Remarkably, in the pre-asymptotic regime our method's estimation variance on time-sensitive parameter $\varphi$ scales faster than the asymptotic Heisenberg limit as a function of depth, $\text{Var}(\hat{\varphi})\approx 1/d^4$. Our work is the first quantum-signal-processing algorithm that demonstrates practical application in laboratory quantum computers.