Multi-mode fiber reservoir computing overcomes shallow neural networks classifiers

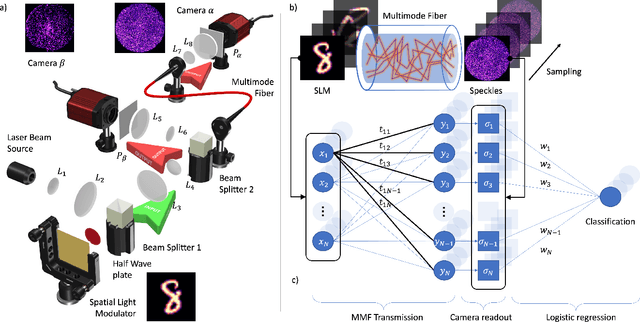
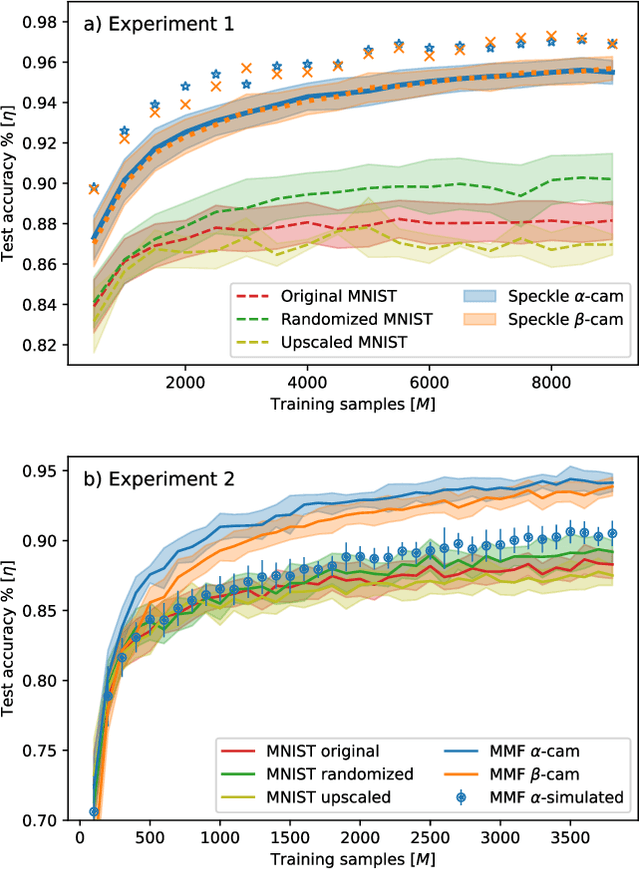
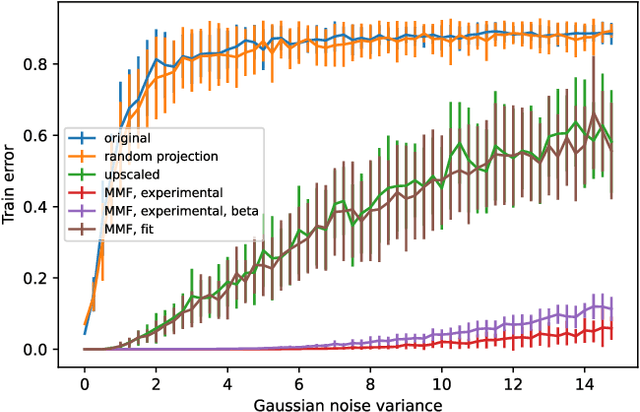
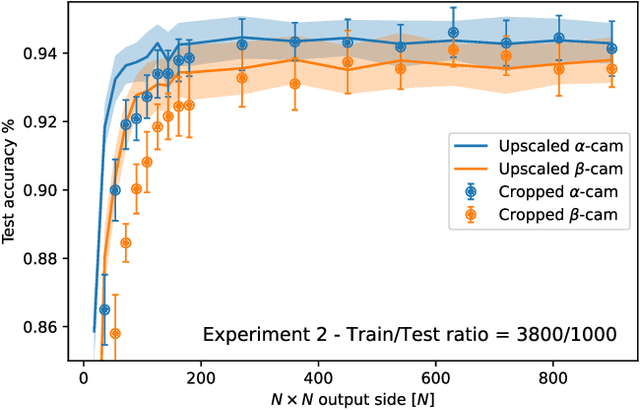
In disordered photonics, one typically tries to characterize the optically opaque material in order to be able to deliver light or perform imaging through it. Among others, multi-mode optical fibers are extensively studied because they are cheap and easy-to-handle complex devices. Here, instead, we use the reservoir computing paradigm to turn these optical tools into random projectors capable of introducing a sufficient amount of interaction to perform non-linear classification. We show that training a single logistic regression layer on the data projected by the fiber improves the accuracy with respect to learning it on the raw images. Surprisingly, the classification accuracy performed with physical measurements is higher than the one obtained using the standard transmission matrix model, a widely accepted tool to describe light transmission through disordered devices. Consistently with the current theory of deep neural networks, we also reveal that the classifier lives in a flatter region of the loss landscape when trained on fiber data. These facts suggest that multi-mode fibers exhibit robust generalization properties, thus making them promising tools for optically-aided machine learning.

Transmission Matrix Inference via Pseudolikelihood Decimation

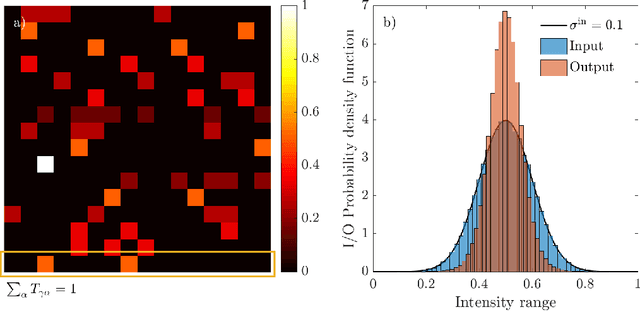
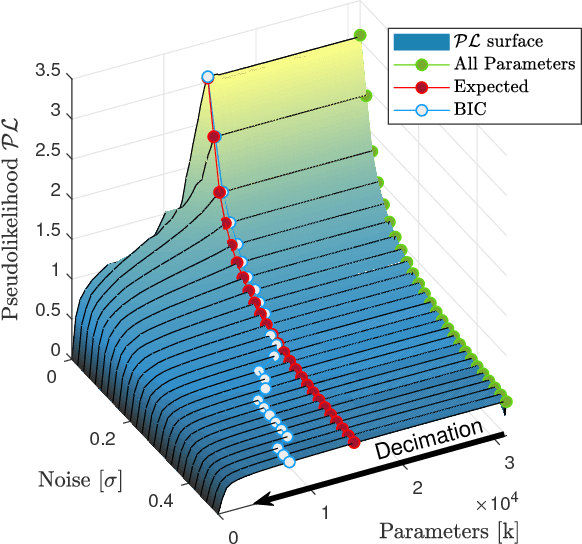
One of the biggest challenges in the field of biomedical imaging is the comprehension and the exploitation of the photon scattering through disordered media. Many studies have pursued the solution to this puzzle, achieving light-focusing control or reconstructing images in complex media. In the present work, we investigate how statistical inference helps the calculation of the transmission matrix in a complex scrambling environment, enabling its usage like a normal optical element. We convert a linear input-output transmission problem into a statistical formulation based on pseudolikelihood maximization, learning the coupling matrix via random sampling of intensity realizations. Our aim is to uncover insights from the scattering problem, encouraging the development of novel imaging techniques for better medical investigations, borrowing a number of statistical tools from spin-glass theory.

Learning Direct and Inverse Transmission Matrices

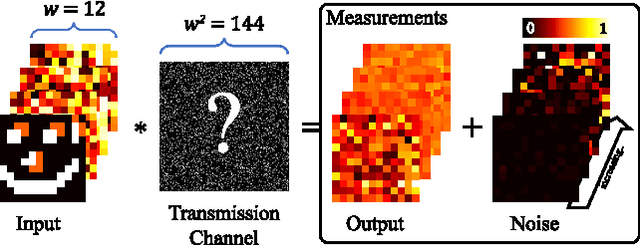
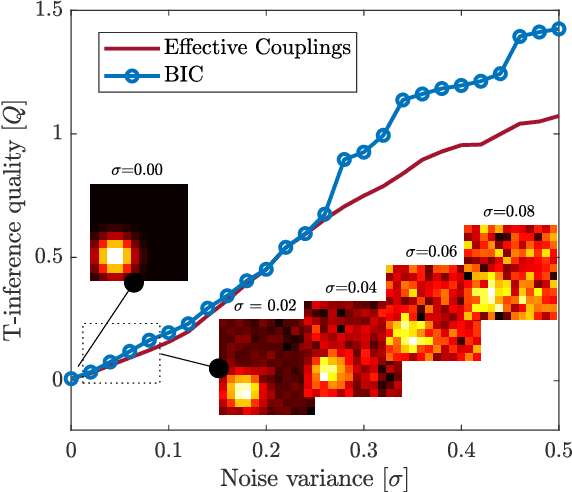
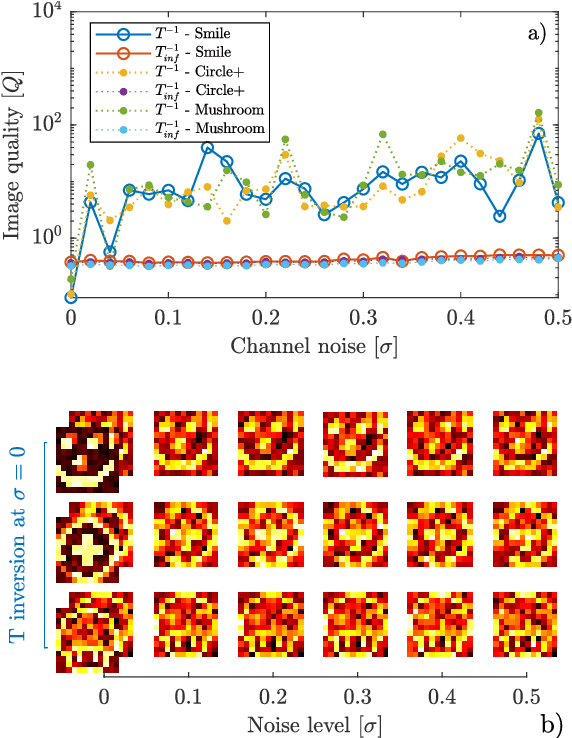
Linear problems appear in a variety of disciplines and their application for the transmission matrix recovery is one of the most stimulating challenges in biomedical imaging. Its knowledge turns any random media into an optical tool that can focus or transmit an image through disorder. Here, converting an input-output problem into a statistical mechanical formulation, we investigate how inference protocols can learn the transmission couplings by pseudolikelihood maximization. Bridging linear regression and thermodynamics let us propose an innovative framework to pursue the solution of the scattering-riddle.