Evidence of Replica Symmetry Breaking under the Nishimori conditions in epidemic inference on graphs

In Bayesian inference, computing the posterior distribution from the data is typically a non-trivial problem, which usually requires approximations such as mean-field approaches or numerical methods, like the Monte Carlo Markov Chain. Being a high-dimensional distribution over a set of correlated variables, the posterior distribution can undergo the notorious replica symmetry breaking transition. When it happens, several mean-field methods and virtually every Monte Carlo scheme can not provide a reasonable approximation to the posterior and its marginals. Replica symmetry is believed to be guaranteed whenever the data is generated with known prior and likelihood distributions, namely under the so-called Nishimori conditions. In this paper, we break this belief, by providing a counter-example showing that, under the Nishimori conditions, replica symmetry breaking arises. Introducing a simple, geometrical model that can be thought of as a patient zero retrieval problem in a highly infectious regime of the epidemic Susceptible-Infectious model, we show that under the Nishimori conditions, there is evidence of replica symmetry breaking. We achieve this result by computing the instability of the replica symmetric cavity method toward the one step replica symmetry broken phase. The origin of this phenomenon -- replica symmetry breaking under the Nishimori conditions -- is likely due to the correlated disorder appearing in the epidemic models.

Inference in conditioned dynamics through causality restoration

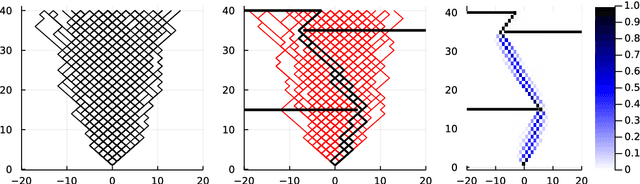
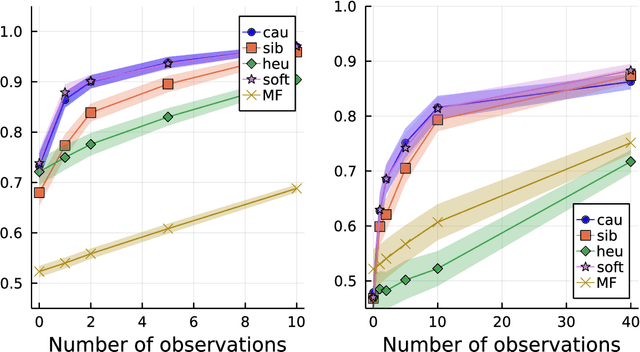
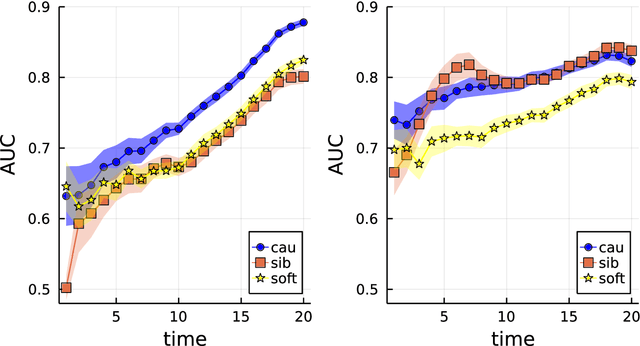
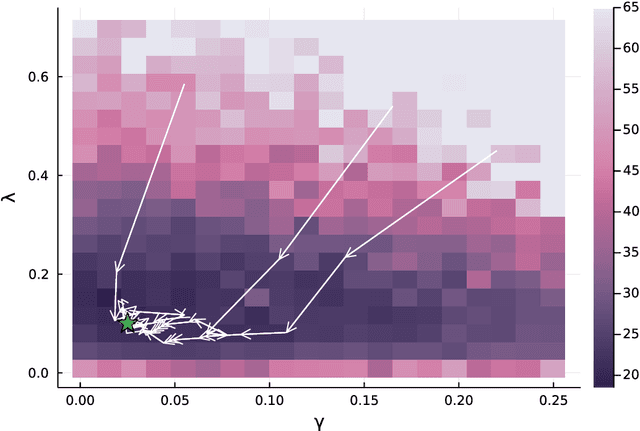
Computing observables from conditioned dynamics is typically computationally hard, because, although obtaining independent samples efficiently from the unconditioned dynamics is usually feasible, generally most of the samples must be discarded (in a form of importance sampling) because they do not satisfy the imposed conditions. Sampling directly from the conditioned distribution is non-trivial, as conditioning breaks the causal properties of the dynamics which ultimately renders the sampling procedure efficient. One standard way of achieving it is through a Metropolis Monte-Carlo procedure, but this procedure is normally slow and a very large number of Monte-Carlo steps is needed to obtain a small number of statistically independent samples. In this work, we propose an alternative method to produce independent samples from a conditioned distribution. The method learns the parameters of a generalized dynamical model that optimally describe the conditioned distribution in a variational sense. The outcome is an effective, unconditioned, dynamical model, from which one can trivially obtain independent samples, effectively restoring causality of the conditioned distribution. The consequences are twofold: on the one hand, it allows us to efficiently compute observables from the conditioned dynamics by simply averaging over independent samples. On the other hand, the method gives an effective unconditioned distribution which is easier to interpret. The method is flexible and can be applied virtually to any dynamics. We discuss an important application of the method, namely the problem of epidemic risk assessment from (imperfect) clinical tests, for a large family of time-continuous epidemic models endowed with a Gillespie-like sampler. We show that the method compares favorably against the state of the art, including the soft-margin approach and mean-field methods.